Question

Tính diện tích đáy của hình chóp tam giác đều

Answer 1

Lời giải:

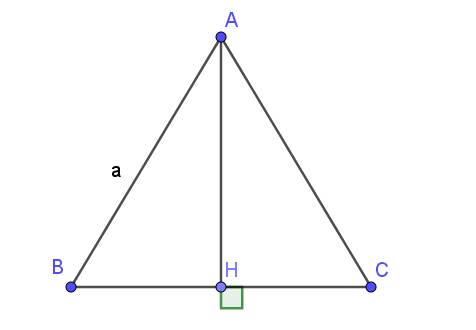
Đáy của hình chóp tam giác đều là tam giác đều. Gọi tam giác đều đó là $ABC$, có độ dài cạnh bằng $a$.

Kẻ $AH\perp BC$ thì do $ABC$ là tam giác đều nên $H$ là trung điểm $BC$

$\Rightarrow HB=\frac{BC}{2}=\frac{a}{2}$
Áp dụng định lý Pitago cho tam giác $ABH$ vuông tại $H$:

$AH=\sqrt{AB^2-BH^2}=\sqrt{a^2-(\frac{a}{2})^2}=\frac{\sqrt{3}a}{2}$

$S_{ABC}=\frac{AH.BC}{2}=\frac{\sqrt{3}a}{2}.a:2=\frac{\sqrt{3}a^2}{4}$

Answer 2

Hình vẽ: