1) A=\(\dfrac{7}{1.3}+\dfrac{7}{3.5}+\dfrac{7}{5.7}+...+\dfrac{7}{99.101}\)=\(\dfrac{7.2}{1.3.2}+\dfrac{7.2}{3.5.2}+\dfrac{7.2}{5.7.2}+...+\dfrac{7.2}{99.101.2}\)=
\(\dfrac{7}{2}\left(\text{}\dfrac{2}{1.3}+\dfrac{2}{3.5}+\dfrac{2}{5.7}+...+\dfrac{2}{99.101}\right)\)=
\(\dfrac{7}{2}\left(\text{}1-\dfrac{1}{3}+\dfrac{1}{3}-\dfrac{1}{5}+\dfrac{1}{5}-\dfrac{1}{7}...+\dfrac{1}{99}-\dfrac{1}{101}\right)\)=
\(\dfrac{7}{2}\left(\text{}1-\dfrac{1}{101}\right)\)=\(\dfrac{7}{2}.\dfrac{100}{101}=\dfrac{350}{101}\)
2) A=\(\dfrac{1}{2}+\dfrac{2}{2.4}+\dfrac{3}{4.7}+\dfrac{4}{7.11}+\dfrac{5}{11.16}\)=\(\dfrac{1}{2}+\dfrac{1}{2}-\dfrac{1}{4}+\dfrac{1}{4}-\dfrac{1}{7}+\dfrac{1}{7}-\dfrac{1}{11}+\dfrac{1}{11}-\dfrac{1}{16}\)
=\(\dfrac{1}{2}+\dfrac{1}{2}-\dfrac{1}{16}\)=\(1-\dfrac{1}{16}=\dfrac{15}{16}\)

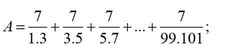
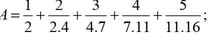



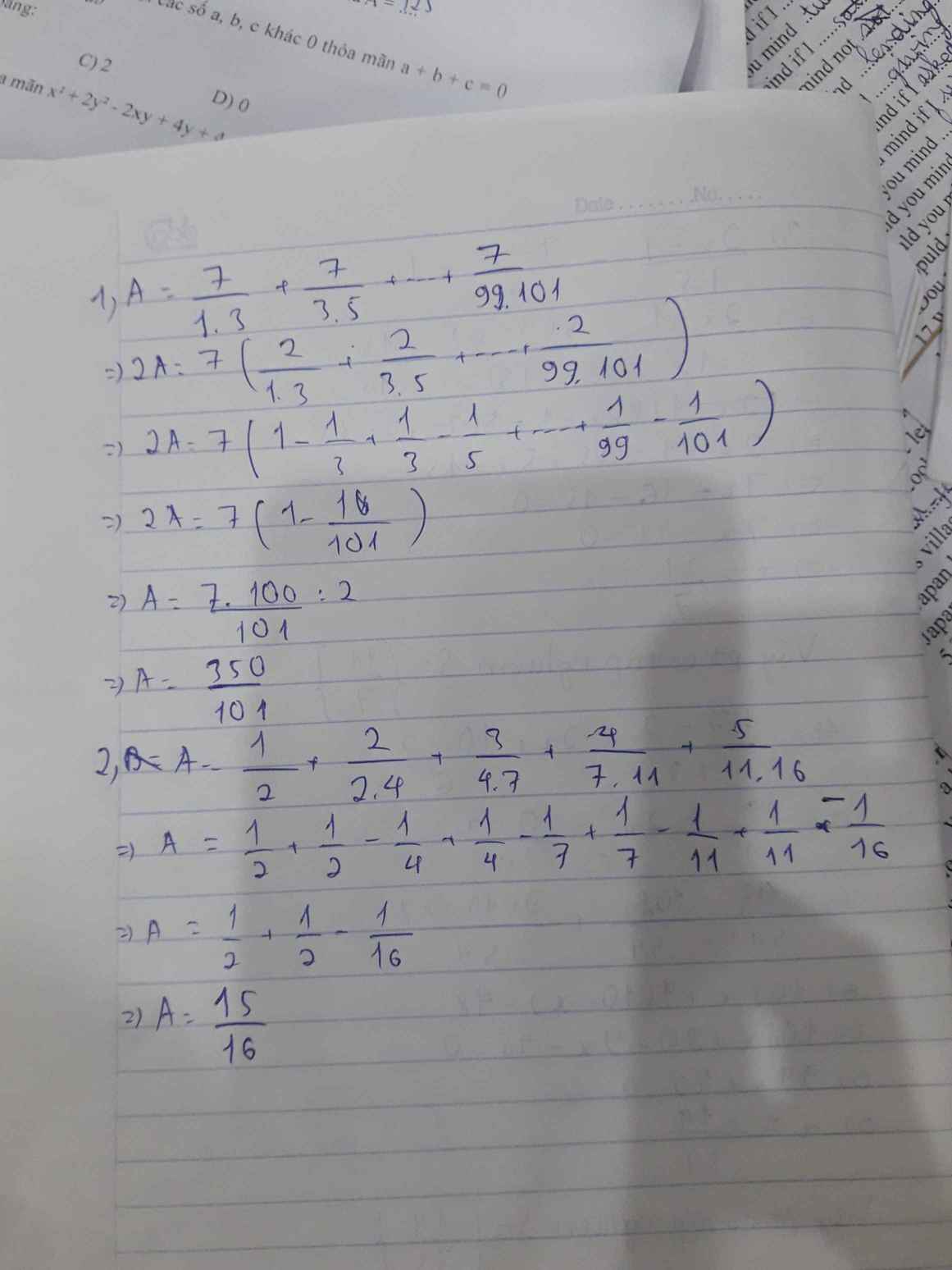



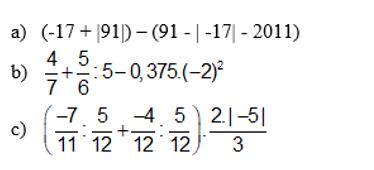

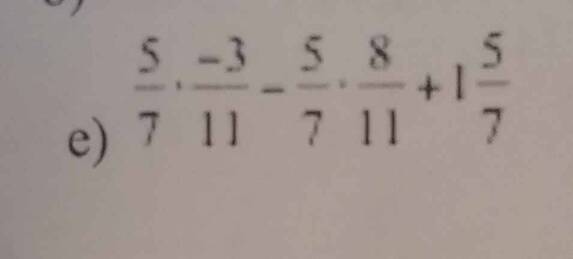 tính cách hợp lí ( nếu có thể )
tính cách hợp lí ( nếu có thể ) 





