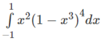Đặt u = 1 – x;
⇒ du = -dx
Đổi biến :
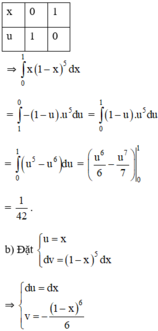
Theo công thức tích phân từng phần:
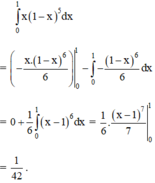
Đặt u = 1 – x;
⇒ du = -dx
Đổi biến :
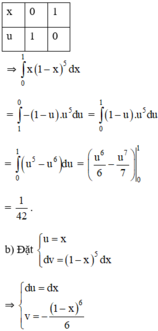
Theo công thức tích phân từng phần:
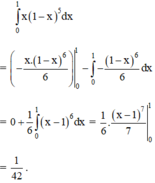
Tính các tích phân sau bằng phương pháp đổi biến số: ∫ 1 2 x 1 - x 5 d x (đặt t = 1 - x)
Tính các tích phân sau bằng phương pháp đổi biến số: ∫ 0 π x sin x 1 + cos 2 x d x (đặt x = π - t)
Tính các nguyên hàm sau bằng phương pháp đổi biến số: ∫ x 2 1 + x 3 3 d x với x > -1 (đặt t = 1 + x 3 )
Áp dụng phương pháp tính tích phân từng phần, hãy tính các tích phân sau: ∫ 1 2 2 1 + x - 1 x e x + 1 x d x
Một hình phẳng được giới hạn bởi y = e - x , y = 0, x = 0, x = 1. Ta chia đoạn [0; 1] thành n phần bằng nhau tạo thành một hình bậc thang (bởi n hình chữ nhật con như Hình bên).
a) Tính diện tích Sn của hình bậc thang (tổng diện tích của n hình chữ nhật con).
b) Tìm 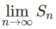 và so sánh với cách tính diện tích hình phẳng này bằng công thức tích phân.
và so sánh với cách tính diện tích hình phẳng này bằng công thức tích phân.
Tính các tích phân sau bằng phương pháp đổi biến số: ∫ 1 9 x 1 - x 3 d x (đặt t = 1 - x 3 )
Tính các tích phân sau bằng phương pháp đổi biến số: ∫ 0 ln 2 e x - 1 d x (đặt t = e x - 1 )
Với cách biến đổi u = 1 + 3 ln x thì tích phân ∫ 1 e ln x x 1 + 3 ln x trở thành
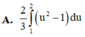
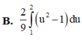
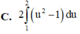
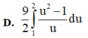
Tính các tích phân sau bằng phương pháp đổi biến số:
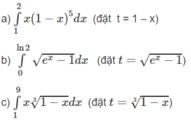
d) 
e)