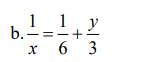\(\dfrac{1}{x}=\dfrac{1}{6}+\dfrac{y}{3}\)
\(\Rightarrow6=x\left(1+2y\right)\)
Vì \(x;y\in Z\Rightarrow x;1+2y\in Z\)
Mà \(1+2y\) là số lẻ `=>` \(x\) là số chẵn
+) TH1:
\(\left\{{}\begin{matrix}x=6\\2y+1=1\end{matrix}\right.\)
`<=>` \(\left\{{}\begin{matrix}x=6\\y=0\end{matrix}\right.\)
+) TH2:
\(\left\{{}\begin{matrix}x=2\\2y+1=3\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x=2\\y=1\end{matrix}\right.\)
+) TH3:
\(\left\{{}\begin{matrix}x=-2\\2y+1=-3\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x=-2\\y=-2\end{matrix}\right.\)
+) TH4:
\(\left\{{}\begin{matrix}x=-6\\2y+1=-1\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x=-6\\y=-1\end{matrix}\right.\)
Cả 4 TH đều thỏa mãn
Vậy...