\(\frac{2x+2}{x-1}\)=\(\frac{2x-2+4}{x-1}\)=2+\(\frac{4}{x-1}\)
U(4)=[-4;-2;-1;1;2;4]
Để PS lớn nhất thì x-1>0 phải bé nhất
Vậy x-1=1
x=2
\(\frac{2x+2}{x-1}\)=\(\frac{2x-2+4}{x-1}\)=2+\(\frac{4}{x-1}\)
U(4)=[-4;-2;-1;1;2;4]
Để PS lớn nhất thì x-1>0 phải bé nhất
Vậy x-1=1
x=2
P=\(\frac{x\sqrt{x}-2x-\sqrt{x}+2}{x\sqrt{x-3\sqrt{x}-2}}+\frac{x\sqrt{x}+2x-\sqrt{3}-2}{x\sqrt{x}-3\sqrt{x}+2}\\ \)
a)Rút gọn P, với giá trị nào của x thì P>1
b)Tìm x nguyên biết P đạt giá trị nguyên lớn nhất
giá trị x nguyên bé nhất và lớn nhất của biểu thức A=\(\frac{3x+2}{2x-1}\) đạt giá trị nguyên là ?
1,Tìm các số nguyên x,y thỏa mãn \(x^2y^2-x^2-3y^2-2x-1=0\).
2,Tìm các số nguyên x,y thỏa mãn \(2x^2+\frac{1}{x^2}+\frac{y^2}{4}=4\) để cho tích xy đạt giá trị lớn nhất.
giá trị x nguyên bé nhất và lớn nhất của biểu thức A=\(\frac{3x+2}{2x-1}\) đạt giá trị nguyên l
Tìm x thuộc Z để 2/A nhận giá trị nguyên dương lớn nhất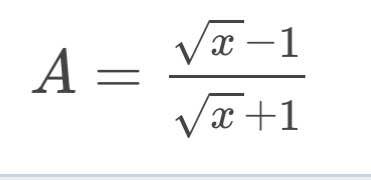
Tìm các cặp số nguyên \(\left(x;y\right)\) thỏa mãn \(2x^2+\dfrac{1}{x^2}+\dfrac{y^2}{4}=4\) sao cho tích \(xy\) đạt giá trị lớn nhất.
\(\frac{x+1}{y^2+1}+\frac{y+1}{z^2+1}+\frac{z+1}{x^2+1}\)
Tìm giá trị lớn nhất của biểu thức trên, biết x+y+z=3
1, Tìm giá trị lớn nhất của biểu thức : \(M=\frac{y\sqrt{x-1}+x\sqrt{y-4}}{xy}\)
2, Tìm tất cả các cặp số nguyên (x;y) thỏa mãn : \(2x^2+y^2+4x=4+2xy\)
3, Cho x,y,z >0 . Chứng minh : \(\frac{x^2}{y^2}+\frac{y^2}{z^2}+\frac{z^2}{x^2}\ge\frac{x}{y}+\frac{y}{z}+\frac{z}{x}\)
Tìm x nguyên để P=\(\frac{3x}{x-\sqrt{x}}\)đạt giá trị lớn nhất