\(=-\left(16x^2-16x-2\right)\)
\(=-\left(16x^2-2\cdot4x\cdot2+4-6\right)\)
\(=-\left(4x-2\right)^2+6\le6\forall x\)
Dấu '=' xảy ra khi \(x=\dfrac{1}{2}\)
\(=-\left(16x^2-16x-2\right)\)
\(=-\left(16x^2-2\cdot4x\cdot2+4-6\right)\)
\(=-\left(4x-2\right)^2+6\le6\forall x\)
Dấu '=' xảy ra khi \(x=\dfrac{1}{2}\)
Tìm x để y=x/(x+2011)^2 đạt GTLN. tìm GTLN đó
Tìm x > 0 để B = \(x = {x \over (x+2011)^2}\) đạt GTLN. TÌm GTLN.
Để tìm thực dương `x` sao cho `P=`\(\dfrac{\sqrt{x}+1}{2-\sqrt{x}}\) đạt GTLN
Tìm x để bt đạt GTLN 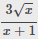
Cho F(x)=\(\sqrt{2-x}+\sqrt{1+x}\). Tìm x để F(x) đạt GTLN
Cho biểu thức A =\(\left(\frac{x+2}{x\sqrt{x}-1}+\frac{\sqrt{x}}{x+\sqrt{x}+1}+\frac{1}{1-\sqrt{x}}\right):\frac{\sqrt{x}-1}{2}\)
Tìm x để A đạt GTLN, tìm GTLN đó
Cho P=1/(x-√x +1) và x lớn hơn hoặc bằng 1
Tìm giá trị của x để P đạt GTLN và tìm GTLN ấy
Tìm giá trị nguyên của x để \(\frac{5}{x+2}\) đạt GTLN ?
Tìm tất cả các giá trị của x để biểu thức B = \(\dfrac{2\sqrt{x}}{x+\sqrt{x}+1}\)\(\left(x\ge0\right)\) đạt GTLN