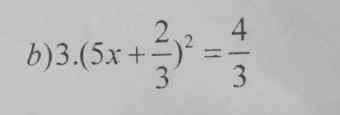\(3.\left(5x+\dfrac{2}{3}\right)^2=\dfrac{4}{3}\)
\(\Rightarrow\left(5x+\dfrac{2}{3}\right)^2=\dfrac{4}{9}\)
\(\Rightarrow\left[{}\begin{matrix}5x+\dfrac{2}{3}=\dfrac{4}{9}\\5x+\dfrac{2}{3}=-\dfrac{4}{9}\end{matrix}\right.\) \(\Rightarrow\left[{}\begin{matrix}5x=-\dfrac{2}{9}\\5x=-\dfrac{10}{9}\end{matrix}\right.\) \(\Rightarrow\left[{}\begin{matrix}x=-\dfrac{2}{45}\\x=-\dfrac{2}{9}\end{matrix}\right.\)
Vậy \(x=\left\{-\dfrac{2}{45};-\dfrac{2}{9}\right\}\)
`3(5x+2/3)^2 = 4/3`
`<=> (5x+2/3)^2 = 4/3 : 3 = 4/(3*3) `
`<=> (5x+2/3)^2 =4/9`
`=> [ (5x+2/3 =2/9),(5x+2/3=-2/9):}`
`<=> [(5x = 2/9 -2/3 =2/9- 4/9 ),(5x = -2/9 - 2/3 = -2/9 - 4/9 = -6/9):}`
`<=>[(5x = -2/9),(5x = -2/3):}`
`<=> [(x = -2/9 : 5 = -2/45),(x =-2/3 : 5 = -2/15):}`
Vậy `x in {-2/45 ; -2/15}`
\(b,3.\left(5x+\dfrac{2}{3}\right)^2=\dfrac{4}{3}\)
\(3.\left(25x^2+\dfrac{4}{9}\right)=\dfrac{4}{3}\)
\(75x^2+\dfrac{4}{3}=\dfrac{4}{3}\)
\(75x^2=\dfrac{4}{3}-\dfrac{4}{3}\)
\(\Rightarrow x=0\)