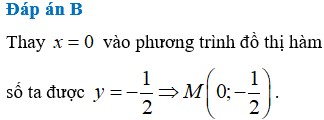Các câu hỏi tương tự
Cho hàm số y f(x) (ax+b)/(cx+d)(a,b,c,d ϵ R;c ≠ 0;d ≠ 0) có đồ thị (C). Đồ thị của hàm số y f’(x) như hình vẽ dưới đây. Biết (C) cắt trục tung tại điểm có tung độ bằng 2. Tiếp tuyến của (C) tại giao điểm của (C) và trục hoành có phương trình là A. x – 3y +2 0 B. x + 3y +2 0 C. x – 3y - 2 0 D. x + 3y -2 0
Đọc tiếp
Cho hàm số y = f(x) =(ax+b)/(cx+d)(a,b,c,d ϵ R;c ≠ 0;d ≠ 0) có đồ thị (C). Đồ thị của hàm số y = f’(x) như hình vẽ dưới đây. Biết (C) cắt trục tung tại điểm có tung độ bằng 2. Tiếp tuyến của (C) tại giao điểm của (C) và trục hoành có phương trình là

A. x – 3y +2 = 0
B. x + 3y +2 = 0
C. x – 3y - 2 = 0
D. x + 3y -2 = 0
cho hàm số \(y=x^2\) và y = -2x+3
a, Vẽ đồ thị của hàm số trên cùng 1 hệ trục tọa độ.
b, Tìm tọa độ giao điểm của 2 đồ thị đó.
Cho (C) là đồ thị của hàm số
y
x
-
3
x
+
1
.
Biết rằng, chỉ có hai điểm thuộc đồ thị (C) cách đều hai điểm A(2;0) và B(0;-2). Gọi các điểm đó lần lượt là M và N. Tìm tọa độ trung điểm I của đoạn thẳng MN. A. I(-1;1) B.
I
0
;
-...
Đọc tiếp
Cho (C) là đồ thị của hàm số y = x - 3 x + 1 . Biết rằng, chỉ có hai điểm thuộc đồ thị (C) cách đều hai điểm A(2;0) và B(0;-2). Gọi các điểm đó lần lượt là M và N. Tìm tọa độ trung điểm I của đoạn thẳng MN.
A. I(-1;1)
B. I 0 ; - 3 2
C. I 0 ; 3 2
D. I(-2;2)
Đồ thị hàm số
y
ax
+
b
x
−
1
cắt trục tung tại điểm A(0;−1), tiếp tuyến của đồ thị tại điểm A có hệ số góc
k
-
3
. Giá trị của của thức Pa+b là A. 1 B. 3 C. 4 D. 2
Đọc tiếp
Đồ thị hàm số y = ax + b x − 1 cắt trục tung tại điểm A(0;−1), tiếp tuyến của đồ thị tại điểm A có hệ số góc k = - 3 . Giá trị của của thức P=a+b là
A. 1
B. 3
C. 4
D. 2
Tính diện tích hình phẳng giới hạn bởi đồ thị hàm số
y
x
3
−
3
x
2
+
1
,
trục tung và tiếp tuyến tại điểm có tọa độ thỏa mãn y 0 A.
∫
0
1
−
x
3
+
3...
Đọc tiếp
Tính diện tích hình phẳng giới hạn bởi đồ thị hàm số y = x 3 − 3 x 2 + 1 , trục tung và tiếp tuyến tại điểm có tọa độ thỏa mãn y'' = 0
A. ∫ 0 1 − x 3 + 3 x 2 − 3 x + 1 dx
B. 2 ∫ 0 1 x 3 − 3 x 2 − 3 x + 1 dx
C. 2 ∫ 0 1 − x 3 + 3 x 2 − 3 x + 1 dx
D. ∫ 0 1 x 3 − 3 x 2 − 3 x + 1 dx
Tìm tọa độ giao điểm M của đồ thị hàm số
y
2
x
-
1
x
+
2
và trục tung A.
M
0
;
-
1
2
B.
M
0
;...
Đọc tiếp
Tìm tọa độ giao điểm M của đồ thị hàm số y = 2 x - 1 x + 2 và trục tung
A. M 0 ; - 1 2
B. M 0 ; - 2
C. M 1 2 ; 0
D. M - 1 2 ; 0
Cho hàm số y
x
-
m
2
x
+
1
(với m là tham số khác 0) có đồ thị (C). Gọi S là diện tích hình phẳng giới hạn bởi đồ thị (C) và hai trục tọa độ. Có bao nhiêu giá trị thực của m thỏa mãn S 1? A. 0. B. 1 C. 2 D. 3.
Đọc tiếp
Cho hàm số y = x - m 2 x + 1 (với m là tham số khác 0) có đồ thị (C). Gọi S là diện tích hình phẳng giới hạn bởi đồ thị (C) và hai trục tọa độ. Có bao nhiêu giá trị thực của m thỏa mãn S = 1?
A. 0.
B. 1
C. 2
D. 3.
Cho hàm số
y
x
−
m
2
x
+
1
(với m là tham số khác 0) có đồ thị là (C). Gọi S là diện tích hình phẳng giới hạn bởi đồ thị (C) và hai trục tọa độ. Có bao nhiêu giá trị thực của m thỏa mãn S 1? A. Hai B. Ba C. Một D. Không
Đọc tiếp
Cho hàm số y = x − m 2 x + 1 (với m là tham số khác 0) có đồ thị là (C). Gọi S là diện tích hình phẳng giới hạn bởi đồ thị (C) và hai trục tọa độ. Có bao nhiêu giá trị thực của m thỏa mãn S = 1?
A. Hai
B. Ba
C. Một
D. Không
Có bao nhiêu giá trị nguyên dương của tham số m để trên đồ thị hàm số (Cm): y1/3 x3+ mx2+(2m-3)m+2019 có hai điểm nằm về hai phía của trục tung mà tiếp tuyến của (Cm) tại hai điểm đó cùng vuông góc với đường thẳng (d): x+2y+60? A. 3 B. 0 C. 2 D. 1
Đọc tiếp
Có bao nhiêu giá trị nguyên dương của tham số m để trên đồ thị hàm số (Cm): y=1/3 x3+ mx2+(2m-3)m+2019 có hai điểm nằm về hai phía của trục tung mà tiếp tuyến của (Cm) tại hai điểm đó cùng vuông góc với đường thẳng (d): x+2y+6=0?
A. 3
B. 0
C. 2
D. 1