Đáp án B
Do điểm M nằm trên trục hoành nên M( x; 0)
Khoảng cách từ M đến mỗi đường thẳng lần lượt là:
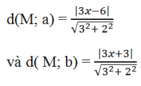
Theo bài ra ta có: d( M; a) = d( M; b) nên
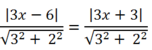
Do đó: ![]()
Sut ra 3x- 6= -3x-3 nên x= 1/2
Vậy điểm M ( 1/2; 0)
Đáp án B
Do điểm M nằm trên trục hoành nên M( x; 0)
Khoảng cách từ M đến mỗi đường thẳng lần lượt là:
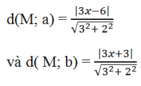
Theo bài ra ta có: d( M; a) = d( M; b) nên
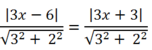
Do đó: ![]()
Sut ra 3x- 6= -3x-3 nên x= 1/2
Vậy điểm M ( 1/2; 0)
Tìm điểm M trên trục hoành sao cho nó cách đều hai đường thẳng: (a) : 3x+ 2y -6= 0 và ( b) : 3x+ 2y + 6= 0 ?
A. (1; 0)
B. (0; 0)
C. (0; 1)
D. (2; 0)
chọn và giải ra luôn nhé Trong mặt phẳng Oxy, phương trình đường thẳng d đi qua A(1;-2) và vuông góc với đường thẳng ∆:3x-2y+x=0 là A. 3x-2y-7=0 B.2x+3y+4=0 C.x+3y+5=0 D.2x+3y-3=0
Trong mặt phẳng với hệ tọa độ Oxy cho tam giác ABC có đỉnh A(2;-3) , B(3:-2) và trọng tâm G nằm trên đường thẳng d: 3x-y-8=0
a, Tìm tọa độ M trên trục hoành sao cho d(M;AB) = \(\sqrt{2}\)
b, tìm tọa độ điểm C biết tam giác ABC có diện tích bằng \(\frac{3}{2}\)
Tìm khoảng cách từ một điểm đến đường thẳng trong các trường hợp sau:
a, A(3; 5) và Δ : 4x + 3y +1 = 0
b, B(1; -2) và d: 3x – 4y -26 = 0
c, C(1; 2) và m: 3x + 4y -11 = 0
Cho A( 2;2) ; B( 5;1) và đường thẳng d: x- 2y + 8= 0. Điểm C nằm trên d và C có hoành độ dương sao cho diện tích tam giác ABC bằng 17. Tọa độ của C là:
A.(8; 10)
B.(12; 10)
C.(6;6)
D.(6; 8)
Tính khoảng cách từ các điểm M(-2; 1) và O(0; 0) đến đường thẳng Δ có phương trình 3x – 2y - 1 = 0.
Cho tam giác ABC và tọa độ một đỉnh và phương trình đường cao.Viết phương trình các cạnh của tam giác đó với:
a, A(3,0),BB'=2x+2y-9=0;CC'=3x-12y-1=0
b,A(1,0), BB'=x-2y+1=0;CC'=3x+y-1=0
Trong mặt phẳng tọa độ Oxy, cho hai điểm A (1; 2) và B (3; 4). Điểm P ( a b ; 0) (với a b là phân số tối giản, b > 0) trên trục hoành thỏa mãn tổng khoảng cách từ P tới hai điểm A và B là nhỏ nhất. Tính S = a + b.
A. S = -2
B. S = 8
C. S = 7
D. S = 4
Cho hàm số y = f(x) = mx + 2m − 3 có đồ thị (d). gọi A, B là hai điểm thuộc đồ thị
và có hoành độ lần lượt là −1 và 2.
1 Xác định tọa độ hai điểm A và B.
2 Tìm m để cả hai điểm A và B cùng nằm phía trên trục hoành.
3 Tìm điều kiện của m để f(x) > 0, ∀x ∈ [−1; 2]