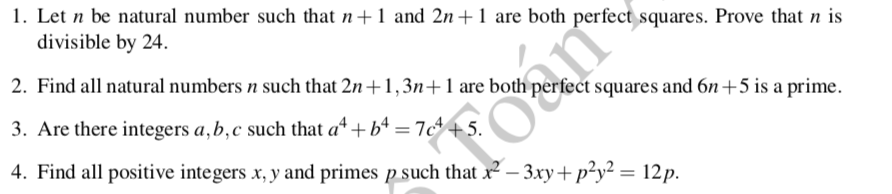Question

Tìm tất cả các số tự nhiên n để n + 1 và n + 13 đều là các số chính phương.

Answer 1

-Vì \(n+1,n+13\) là các số chính phương nên đặt \(n+1=a^2,n+13=b^2\)

\(\Rightarrow b^2-a^2=n+13-\left(n+1\right)=12\)

\(\Rightarrow\left(b-a\right)\left(b+a\right)=12=\left[{}\begin{matrix}1.12\\2.6\\3.4\end{matrix}\right.\)

-Vì \(b-a< b+a\)

\(\Rightarrow\left[{}\begin{matrix}b-a=1;b+a=12\\b-a=2;b+a=6\\b-a=3;b+a=4\end{matrix}\right.\)

\(\Rightarrow\left[{}\begin{matrix}b=\dfrac{13}{2};a=\dfrac{11}{2}\left(loại\right)\\b=4;a=2\left(nhận\right)\\b=\dfrac{7}{2};a=\dfrac{1}{2}\left(loại\right)\end{matrix}\right.\)

-Vậy \(n=3\) thì n+1 và n+12 đều là các số chính phương.