Chọn B
Đặt ![]() ta có
ta có ![]()
![]()
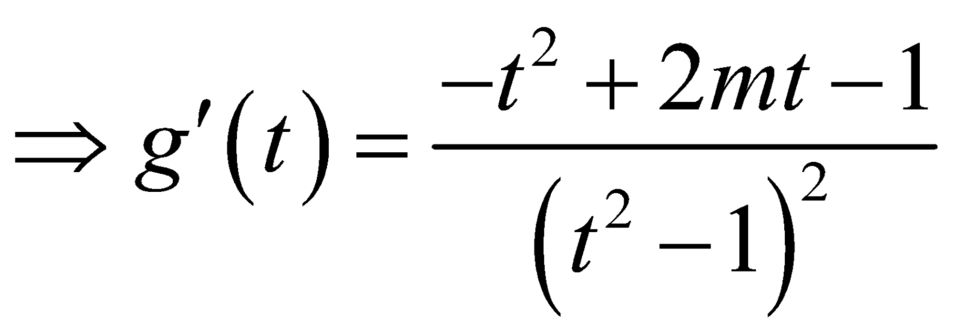 để hàm số nghịch biến trên khoảng
để hàm số nghịch biến trên khoảng ![]() thì
thì ![]()
![]() .
.
Th1: ![]()
![]()
![]() .
.
Th2:![]() để
để ![]() thì
thì ![]()
![]()
![]() hay
hay ![]() .
.
Th3: ![]() để
để ![]() thì
thì ![]()
![]() hay
hay ![]() .
.
Vậy ![]() .
.
Chọn B
Đặt ![]() ta có
ta có ![]()
![]()
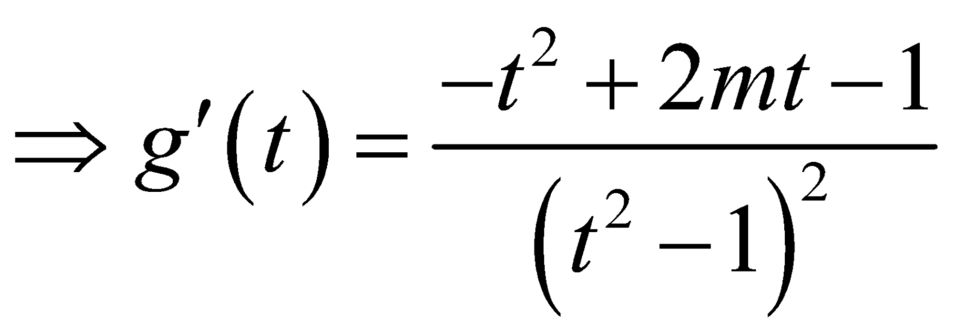 để hàm số nghịch biến trên khoảng
để hàm số nghịch biến trên khoảng ![]() thì
thì ![]()
![]() .
.
Th1: ![]()
![]()
![]() .
.
Th2:![]() để
để ![]() thì
thì ![]()
![]()
![]() hay
hay ![]() .
.
Th3: ![]() để
để ![]() thì
thì ![]()
![]() hay
hay ![]() .
.
Vậy ![]() .
.
Tìm tất cả giá trị thực của tham số m sao cho hàm số y = f ( x ) = m - 2 sin x 1 + cos 2 x nghịch biến trên khoảng (0; π / 6 )
A.![]() .
.
B.![]() .
.
C.![]() .
.
D.![]() .
.
Tìm tất cả các giá trị thực của tham số m sao cho hàm số y= (m-3)x- (2m+1).cos x luôn nghịch biến trên R?
A. - 4 ≤ m ≤ 2 3
B. m> 2
C. m > 3 m ≠ 1
D. m<2
Tìm tất cả các giá trị thực của tham số m để hàm số y = - x 3 + 2 x 2 - ( m - 1 ) x + 2 nghịch biến trên khoảng (-∞;+∞)
A. m ≤ 7 3
B. m ≥ 7 3
C. m ≥ 1 3
D. m > 7 3
Tìm tất cả các giá trị thực của tham số m sao cho hàm số y = m x + 2 m + 1 x - m nghịch biến trên khoảng (0;+¥)
![]()
![]()
![]()
![]()
Tìm tất cả các giá trị thực của tham số m để hàm số y = sin x + m sin x - 1 nghịch biến trong khoảng ( π 2 ; π )
A. ![]()
B. ![]()
C. ![]()
D. ![]()
Tìm tất cả các giá trị thực của tham số m để hàm số y = m x - 4 m - x nghịch biến trên khoảng (-3;1)
![]()
![]()
![]()
![]()
Tìm tất cả các giá trị thực của tham số m để hàm số y = x + 2 - m x + 1 nghịch biến trên các khoảng mà nó xác định?
A. m ≤ -1
B. m < 1.
C. m < -3.
D. m ≤ -3
Tìm tất cả các giá trị thực của tham số m để hàm số y = x + 2 - m x + 1 nghịch biến trên mỗi khoảng xác định của nó.
![]()
![]()
![]()
![]()
Cho hàm số y = f(x) liên tục trên R và có đồ thị như hình vẽ. Tập hợp tất cả các giá trị thực của tham số m để phương trình f(sin x) = m có nghiệm thuộc khoảng 0 ; π là

![]()
![]()
![]()
![]()