Các câu hỏi tương tự
Tìm tất cả các giá trị thực của tham số m để hàm số
y
−
2
x
3
+
3
m
x
2
−
1
đạt cực tiểu tại x 0. A. m 0 B.
m
1
2
C. m0 D.
m
1
2
Đọc tiếp
Tìm tất cả các giá trị thực của tham số m để hàm số y = − 2 x 3 + 3 m x 2 − 1 đạt cực tiểu tại x= 0.
A. m > 0
B. m > 1 2
C. m<0
D. m < 1 2
Tìm tất cả các giá trị thực của tham số m để hàm số
y
x
4
−
2
m
+
1
x
2
+
m
2
−
1
đạt cực tiểu tại
x
0.
A. m-1 B. m-1 C.
m
≤
−
1.
D.
m...
Đọc tiếp
Tìm tất cả các giá trị thực của tham số m để hàm số y = x 4 − 2 m + 1 x 2 + m 2 − 1 đạt cực tiểu tại x = 0.
A. m<-1
B. m=-1
C. m ≤ − 1.
D. m ≤ − 1 m ≥ 1
Tìm tất cả các giá trị thực của tham số m để bất phương trình
(
m
+
1
)
x
2
-
2
(
m
+
1
)
x
+
4
≥
0
(
1
)
có tập nghiệm
S
ℝ
?
A.
m
-
1
B.
-
1
≤...
Đọc tiếp
Tìm tất cả các giá trị thực của tham số m để bất phương trình ( m + 1 ) x 2 - 2 ( m + 1 ) x + 4 ≥ 0 ( 1 ) có tập nghiệm S = ℝ ?
A. m > - 1
B. - 1 ≤ m ≤ 3
C. - 1 < m ≤ 3
D. - 1 < m < 3
Tìm tất cả các giá trị thực của tham số m để hàm số
y
1
3
x
3
-
(
m
-
1
)
x
2
+
4
(
m
-
2
)
x
+
2
có hai cực trị
x
1
,
x
2
thỏa mãn
x
2...
Đọc tiếp
Tìm tất cả các giá trị thực của tham số m để hàm số y = 1 3 x 3 - ( m - 1 ) x 2 + 4 ( m - 2 ) x + 2 có hai cực trị x 1 , x 2 thỏa mãn x 2 1 + x 2 2 + 3 x 1 x 2 = 4
A. m= -2 hoặc m = -1
B. m = -1 hoặc m = 2
C. m = - 1 ± 21
D. Không tồn tại m
Tìm tất cả các giá trị tham số m để hàm số
y
x
2
+
(
2
-
m
)
x
-
m
+
2
x
+
1
c...
Đọc tiếp
Tìm tất cả các giá trị tham số m để hàm số y = x 2 + ( 2 - m ) x - m + 2 x + 1 có 4 cực trị.
A. - 2 ≤ m ≤ 3 .
B. - 2 < m ≤ 3 .
C. m> 2 hoặc m< -2
D. m> 2 hoặc m< -3
Tìm tất cả giá trị của tham số m để hàm số
y
x
-
m
+
2
x
-
m
-
1
xác định trên
0
;
+
∞
. A.
m
≤
1
B.
m
≥
1
C. m 1 D.
m
≤
-
1
Đọc tiếp
Tìm tất cả giá trị của tham số m để hàm số y = x - m + 2 x - m - 1 xác định trên 0 ; + ∞ .
A. m ≤ 1
B. m ≥ 1
C. m < 1
D. m ≤ - 1
Cho hàm số
y
f
x
có đồ thị như hình vẽ . Tìm tất cả các giá trị thực của tham số m để phương trình
f
x
−
m
0
có đúng 2 nghiệm và giá trị tuyệt đối của 2 nghiệm này đều lớn hơn 1 A.
m
−
4
B.
−
4
m
−
3
C.
m...
Đọc tiếp
Cho hàm số y = f x có đồ thị như hình vẽ . Tìm tất cả các giá trị thực của tham số m để phương trình f x − m = 0 có đúng 2 nghiệm và giá trị tuyệt đối của 2 nghiệm này đều lớn hơn 1
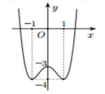
A. m > − 4
B. − 4 < m < − 3
C. m > − 3
D. − 4 < m ≤ − 3
Cho hàm số
f
(
x
)
x
3
–
(
2
m
-
1
)
x
2
+
(
2
-
m
)
x
+
2
. Tìm tất cả các giá trị thực của tham số m để hàm số yf(|x|) có 5 cực trị A.
-
10
m
5
4
B.
-...
Đọc tiếp
Cho hàm số f ( x ) = x 3 – ( 2 m - 1 ) x 2 + ( 2 - m ) x + 2 . Tìm tất cả các giá trị thực của tham số m để hàm số y=f(|x|) có 5 cực trị
A. - 10 < m < 5 4
B. - 2 < m < 5
C. - 2 < m < 5 4
D. 5 4 < m < 2
Cho hàm số y f (x) có đạo hàm liên tục trên
ℝ
, với f (x) 0 và f (0) 1. Biết rằng
f
(
x
)
+
3
x
x
-
2
f
(
x
)
0
,
∀
x
∈
ℝ
. Tìm tất cả các giá trị thực của tham số m để phương trình
f
x
+
m
0
có bốn nghiệm thực phân biệt. A.
1...
Đọc tiếp
Cho hàm số y = f (x) có đạo hàm liên tục trên ℝ , với f (x) > 0 và f (0) = 1. Biết rằng f ' ( x ) + 3 x x - 2 f ( x ) = 0 , ∀ x ∈ ℝ . Tìm tất cả các giá trị thực của tham số m để phương trình f x + m = 0 có bốn nghiệm thực phân biệt.
A. 1 < m < e 4
B. - e 6 < m < - 1
C. - e 4 < m < - 1
D. 0 < m < e 4