Chọn A.
Phương pháp: Viết và giải các điều kiện xác định.
Lưu ý: Với toán trắc nghiệm thì có thể thử phương án để loại ba phương án sai.
Cách giải: Ta có điều kiện xác định hàm số:
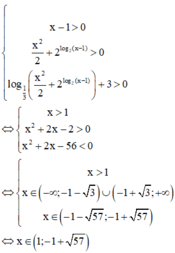
Chọn A.
Phương pháp: Viết và giải các điều kiện xác định.
Lưu ý: Với toán trắc nghiệm thì có thể thử phương án để loại ba phương án sai.
Cách giải: Ta có điều kiện xác định hàm số:
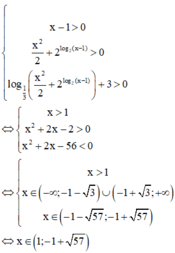
Tìm tập xác định của hàm số y = log x 2 - x - 2
A. - ∞ ; 2
B. 1 ; + ∞
C. - ∞ ; - 1 ∪ 2 ; + ∞
D. - 1 ; 1
Tìm tập xác định của hàm số y=log ( x2-x-2)
![]()
![]()
![]()
![]()
Tìm tập xác định của hàm số y = log - 2 x 2 + 5 x - 2
A. 1 2 ; 2
B. ( - ∞ ; 1 2 ] ∪ [ 2 ; + ∞ )
C. - ∞ ; 1 2 ∪ 2 , + ∞
D. 1 2 ; 2
Tập xác định của hàm số y = l o g ( x 2 - 1 ) là
A. - ∞ ; - 1 ∪ 1 + ∞
B. - ∞ ; 1
C. 1 + ∞
D. (-1;1)
Cho x ϵ (0;π/2). Biết log(sinx)+log(cosx)=-1 và log(sinx+cosx)=1/2(logn-1). Giá trị của n là
A. 11.
B. 12.
C. 10.
D. 15.
Cho hàm số y = ( x - 2 ) - 1 2 Bạn Toán tìm tập xác định của hàm số bằng cách như sau:
Bước 1: Ta có y = 1 ( x - 2 ) 1 2 = 1 x - 2
Bước 2: Hàm số xác định ⇔ x - 2 > 0 ⇔ x > 2
Bước 3: Vậy tập xác định của hàm số là D = ( 2 ; + ∞ )
Lời giải trên của bạn toán đúng hay sai? Nếu sai thì sai ở bước nào?
A. Bước 3
B. Bước 1
C. Đúng
D. Bước 2
Đạo hàm của hàm số y = log ( 1 - x ) bằng
A. 1 ( x - 1 ) ln 10
B. 1 x - 1
C. 1 1 - x
D. - 1 ( x - 1 ) ln 10
Đạo hàm của hàm số y=log(1-x) là
A. 1 x - 1 ln 10
B. 1 1 - x
C. 1 1 - x ln 10
D. 1 x - 1
Tìm số nghiệm của phương trình x - 1 2 e x - 1 - log 2 = 0
A. 4
B. 3
C. 2
D. 0
Cho các phát biểu sau
(1) Đơn giản biểu thức M = a 1 4 - b 1 4 a 1 4 + b 1 4 a 1 2 + b 1 2 ta được M = a - b
(2) Tập xác định D của hàm số y = log 2 ln 2 x - 1 là D = e ; + ∞
(3) Đạo hàm của hàm số y = log 2 ln x là y ' = 1 x ln x . ln 2
(4) Hàm số y = 10 log a x - 1 có đạo hàm tại mọi điểm thuộc tập xác định
Số các phát biểu đúng là
A. 6
B. 1
C. 3
D. 4