Điều kiện: 3 - 2x ≥ 0 ⇔ 3 ≥ 2x ⇔ x ≤ 1,5
Ta có: 3 - 2 x ≥ 5 ⇔ 3 - 2x ≤ 5 ⇔ -2x ≤ 2 ⇔ x ≥ -1
Kết hợp với điều kiện ta có: -1 ≤ x ≤ 1,5
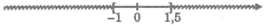
Điều kiện: 3 - 2x ≥ 0 ⇔ 3 ≥ 2x ⇔ x ≤ 1,5
Ta có: 3 - 2 x ≥ 5 ⇔ 3 - 2x ≤ 5 ⇔ -2x ≤ 2 ⇔ x ≥ -1
Kết hợp với điều kiện ta có: -1 ≤ x ≤ 1,5
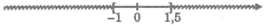
Tìm tập hợp các giá trị x thỏa mãn điều kiện sau và biểu diễn tập hợp đó trên trục số: x - 2 ≥ 3
Tìm tập hợp các giá trị x thỏa mãn điều kiện sau và biểu diễn tập hợp đó trên trục số: x 3 ≥ 2
Tìm tập hợp các giá trị x thỏa mãn điều kiện sau và biểu diễn tập hợp đó trên trục số: x 3 ≤ - 1 , 5
Tìm tập hợp các số x thỏa mãn bất đẳng thức x < 3 và biểu diễn tập hợp đó trên trục số
Tìm tập hợp các số x thỏa mãn bất đẳng thức x > 2 và biểu diễn tập hợp đó trên trục số
cho các số thực x và y thỏa mãn điều kiện x^2 + y^2 = 2 Tìm giá trị nhỏ nhất của biểu thức P = 3(x+y)+xy
Cho hàm số y = ( k - 3 )x + k' ( d ) . Tìm các giá trị của k và k' để đường thẳng ( d ) thỏa mãn một trong các điều kiện sau
a. Đi qua điểm A( 1 ; 2 ) và B( -3 ; 4 )
b. Cắt trục tung tại điểm có tung độ bằng 1-√2 và cắt trục hoành tại điểm 1 + √2
c. Cắt đường thẳng 2y - 4x + 5 = 0
d. Song song với đường thẳng y - 2x -1 =0
e. Trùng với đường thẳng 3x + y - 5 = 0
Tập hợp các giá trị của x thỏa mãn (x-1)^2=2016. |x-1| là {.....}
\(\text{Các số thực không âm x,y,z thay đổi thỏa mãn điều kiện: x^2+ y^2+x^2+x^2y^2+y^2z^2+z^2x^2=6. \text{Tìm giá trị lớn nhất và nhỏ nhất của biểu thức Q=x+y+z}}\)\(\text{Các số thực không âm x,y,z thay đổi thỏa mãn điều kiện x^2+y^2+z^2+x^2y^2+y^2z^2+z^2x^2=6. Tìm giá trị lớn nhất và nhỏ nhất của biểu thức Q=x+y+z}\)