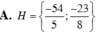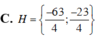Các câu hỏi tương tự
MỌI NGƯỜI GIÚP MÌNH MÔN TIN VỚI Ạ!Cho dãy số (a1, a2, a3, ..., an) là một hoán vị bất kỳ của tập hợp (1, 2, 3, ..., n). Dãy số (b1, b2, b3, ..., bn) gọi là nghịch thế của dãy a nếu bi là số phần tử đứng trước số i trong dãy a mà lớn hơn i.Ví dụ:Dãy a là: 3 2 5 7 1 4 6Dãy b là: 4 1 0 2 0 1 0a. Cho dãy a, hãy xây dựng chương trình tìm dãy b.b. Cho dãy b, xây dựng chương trình tìm dãy a.Dữ liệu vào: Trong file NGICH.INP với nội dung:-Dòng đầu tiên là số n (1 n 10 000).-Các dòng tiếp theo là n số...
Đọc tiếp
MỌI NGƯỜI GIÚP MÌNH MÔN TIN VỚI Ạ!
Cho dãy số (a1, a2, a3, ..., an) là một hoán vị bất kỳ của tập hợp (1, 2, 3, ..., n). Dãy số (b1, b2, b3, ..., bn) gọi là nghịch thế của dãy a nếu bi là số phần tử đứng trước số i trong dãy a mà lớn hơn i.
Ví dụ:
Dãy a là: 3 2 5 7 1 4 6
Dãy b là: 4 1 0 2 0 1 0
a. Cho dãy a, hãy xây dựng chương trình tìm dãy b.
b. Cho dãy b, xây dựng chương trình tìm dãy a.
Dữ liệu vào: Trong file NGICH.INP với nội dung:
-Dòng đầu tiên là số n (1 <= n <= 10 000).
-Các dòng tiếp theo là n số của dãy a, mỗi số cách nhau một dấu cách,
-Các dòng tiếp theo là n số của dãy b, mỗi số cách nhau bởi một dấu cách.
Dữ liệu ra: Trong file NGHICH.OUT với nội dung:
-N số đầu tiên là kết quả của câu a
-Tiếp đó là một dòng trống và sau đó là n số kết quả của câu b (nếu tìm được dãy a).
Tìm tập hợp các số âm trong dãy số.
x
1
;
x
2
;
x
3
;
.
.
.
;
x
n
với
x
n
A
n
+
1
4
P...
Đọc tiếp
Tìm tập hợp các số âm trong dãy số. x 1 ; x 2 ; x 3 ; . . . ; x n với x n = A n + 1 4 P n + 2 - 143 4 P n , n ∈ ℕ *
A. H = - 54 5 ; - 23 8
B. H = 1 ; 2
C. H = - 63 4 ; - 23 4
D. Đáp án khác
Biết rằng hệ số xn-2 trong khai triển \(\left(x-\frac{1}{4}\right)^n\)bằng 31.Tìm n
Câu 1: Tính giới hạn a, limdfrac{2-5^{n-2}}{3^n2.5^n} b,limdfrac{2-5^{n+2}}{3^n-2.5^n}Câu 2 :CMR :x^4+x^3-3x^2+x+10 có ít nhất một nghiệm âm lớn hơn -1Câu 3: Cho hình chóp S.ABCD có đáy là hình vuông cạnh a và các cạnh bên đều bằng a. Gọi M,N lần lượt là trung điểm của AD và SD. Tìm số đo góc giữa 2 đường thẳng MN và SC
Đọc tiếp
Câu 1: Tính giới hạn
a, lim\(\dfrac{2-5^{n-2}}{3^n=2.5^n}\) b,lim\(\dfrac{2-5^{n+2}}{3^n-2.5^n}\)
Câu 2 :CMR :\(x^4+x^3-3x^2+x+1=0\) có ít nhất một nghiệm âm lớn hơn -1
Câu 3: Cho hình chóp S.ABCD có đáy là hình vuông cạnh a và các cạnh bên đều bằng a. Gọi M,N lần lượt là trung điểm của AD và SD. Tìm số đo góc giữa 2 đường thẳng MN và SC
Cho đa thức \(P\left(x\right)=x^n+a_{n-1}x^{n-1}+...+a_1x+1\) có các hệ số không âm. CMR nếu \(P\left(x\right)\) có \(n\) nghiệm thực thì \(P\left(2\right)\ge3^n\)
1.lim(frac{1}{1.2}+frac{1}{2.3}+frac{1}{3.4}+....+frac{1}{nleft(n+1right)})2.Tìm tất cả các giá trị của a sao cho limfrac{4^n+a.5^n}{left(2a-1right).5^n+2^n}13. Cho ain Rvà lim(sqrt{n^2+an+4}-n+15).Tìm a4.ChoLim_{(x-2)}fleft(xright)5. Tìm giới hạn lim_{left(x-2right)}sqrt{[fleft(xright)-3]x}
Đọc tiếp
1.lim(\(\frac{1}{1.2}+\frac{1}{2.3}+\frac{1}{3.4}+....+\frac{1}{n\left(n+1\right)}\))
2.Tìm tất cả các giá trị của a sao cho lim\(\frac{4^n+a.5^n}{\left(2a-1\right).5^n+2^n}\)=1
3. Cho \(a\in R\)và lim(\(\sqrt{n^2+an+4}-n+1=5\)).Tìm a
4.Cho\(Lim_{(x->2)}f\left(x\right)=5\). Tìm giới hạn \(lim_{\left(x->2\right)}\sqrt{[f\left(x\right)-3]x}\)
Tìm số hạng chứa x5 trong khai triển \(\left(x-\dfrac{2}{x}\right)^{n^{ }}\) , biết n là số tự nhiên thỏa mãn \(C^3_n=\dfrac{4}{3}n+2C^2_n\)
A.144 B.134 C.115 D.141
Cho tập hợp X{0;1;2;3;4;5;6;7;8;9}, người ta lập 2 tập hợp con của X, tập hợp A{0;1;2;...;n} gồm n+1 số tự nhiên đầu tiên và B{n+1;n+2;...;2n}. Từ mỗi tập hợp A và B đó, người ta lập số tự nhiên có 5 chữ số đôi một khác nhau, trong số đó có hai chữ số hàng chục nghìn và hàng nghìn được viết bởi các chữ số lấy trong tập hợp A, 3 chữ số còn lại được lấy trong tập hợp B. Hỏi lập được bao nhiêu số tự nhiên như vậy và số lớn nhất là bao nhiêu?
Đọc tiếp
Cho tập hợp X={0;1;2;3;4;5;6;7;8;9}, người ta lập 2 tập hợp con của X, tập hợp A={0;1;2;...;n} gồm n+1 số tự nhiên đầu tiên và B={n+1;n+2;...;2n}. Từ mỗi tập hợp A và B đó, người ta lập số tự nhiên có 5 chữ số đôi một khác nhau, trong số đó có hai chữ số hàng chục nghìn và hàng nghìn được viết bởi các chữ số lấy trong tập hợp A, 3 chữ số còn lại được lấy trong tập hợp B. Hỏi lập được bao nhiêu số tự nhiên như vậy và số lớn nhất là bao nhiêu?
1/ Giải phương trình sau:tan^2left(x+dfrac{pi}{3}right)+left(sqrt{3}-1right)tanleft(x+dfrac{pi}{3}right)-sqrt{3}02/ Tìm hệ số của số hạng chứa x^{26} trong khai triển left(dfrac{1}{x^4}+x^7right)^n . Biết C^2_{n+2}-4C^n_{n+1}2left(n+1right) (n ∈ N* ; x 0)
Đọc tiếp
1/ Giải phương trình sau:
\(tan^2\left(x+\dfrac{\pi}{3}\right)+\left(\sqrt{3}-1\right)tan\left(x+\dfrac{\pi}{3}\right)-\sqrt{3}=0\)
2/ Tìm hệ số của số hạng chứa \(x^{26}\) trong khai triển \(\left(\dfrac{1}{x^4}+x^7\right)^n\) . Biết \(C^2_{n+2}-4C^n_{n+1}=2\left(n+1\right)\) (n ∈ N* ; x > 0)