Đặt z = x + yi , ta được hệ phương trình:
Vậy z = 1 + i.
Đúng 0
Bình luận (0)
Các câu hỏi tương tự
Tìm số phức z thỏa mãn hệ phương trình:
z
-
2
i
z
z
-
i...
Đọc tiếp
Tìm số phức z thỏa mãn hệ phương trình:
z - 2 i = z z - i = z - 1
Số phức thỏa mãn phương trình
z
+
3
z
¯
(
2
+
i
)
3
(
2
-
i
)
Mô đun của số phức
w
z
+
10
i
là
Đọc tiếp
Số phức thỏa mãn phương trình z + 3 z ¯ = ( 2 + i ) 3 ( 2 - i ) Mô đun của số phức w = z + 10 i là
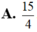
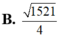
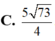
Trên mặt phẳng phức tập hợp các số phức z = x + yi thỏa mãn |z + 2 - i| = | z ¯ - 3i| là đường thẳng có phương trình
A. y = x + 1
B. y = -x + 1
C. y = -x - 1
D. y = x - 1
Cho số phức z thay đổi hoàn toàn thỏa mãn: |z-i| = |z-1+2i|. Tập hợp các điểm trên mặt phẳng tọa độ biểu diễn số phức w thỏa mãn: w = (2-i)z+1 là một đường thẳng. Viết phương trình đường thẳng đó.
A. -x + 7y + 9 = 0
B. x + 7y - 9 = 0
C. x + 7y + 9 = 0
D. x - 7y + 9 = 0
Tìm số phức z thỏa mãn hệ thức
z
-
2
+
i
10
v
à
z
.
z
¯
25
A. z 3 + 4i; z 5. B. z 3 + 4i; z -5. C. z -3 + 4i;z 5. D. z 3 - 4i; z -5.
Đọc tiếp
Tìm số phức z thỏa mãn hệ thức z - 2 + i = 10 v à z . z ¯ = 25
A. z = 3 + 4i; z = 5.
B. z = 3 + 4i; z= -5.
C. z = -3 + 4i;z = 5.
D. z = 3 - 4i; z = -5.
Tính tổng các phần ảo của các số phức z thỏa mãn phương trình z + 2 z ¯ 3 = 8
A. 0.
B. 1.
C. 2.
D. 4.
Biết số phức z thỏa mãn phương trình z + 1 z = 1 . Tính giá trị biểu thức P = z 2016 + 1 z 2016
A. 0
B. 1
C. 2
D. 3
Cho số phức z thỏa mãn phương trình 4|z+i| + 3|z-i| = 10. Tính giá trị nhỏ nhất của |z|
A. 1 2
B. 5 7
C. 3 2
D. 1
Cho số phức thỏa mãn
z
-
i
z
-
1
+
2
i
. Tập hợp điểm biểu diễn số phức w (2 - i) z +1 trên mặt phẳng phức là một đường thẳng. Phương trình của đường thẳng đó là
Đọc tiếp
Cho số phức thỏa mãn z - i = z - 1 + 2 i . Tập hợp điểm biểu diễn số phức w = (2 - i) z +1 trên mặt phẳng phức là một đường thẳng. Phương trình của đường thẳng đó là
