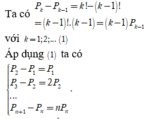
Cộng các đẳng thức ở (2) ta được ![]()
Do
P
1
=
1
![]()
Theo đề, ta có ![]()
Chọn A.
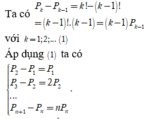
Cộng các đẳng thức ở (2) ta được ![]()
Do
P
1
=
1
![]()
Theo đề, ta có ![]()
Chọn A.
Cho i là đơn vị ảo. Gọi S là tập hợp các số nguyên dương n có 2 chữ số thỏa mãn in là số nguyên dương. Số phần tử của S là
A. 22
B. 23
C. 45
D. 46
Với n là số nguyên dương thỏa mãn A n k + 2 A n 2 = 100 ( A n k là số các chỉnh hợp chập k của tập hợp có n phần tử). Số hạng chứa x 5 trong khai triển của biểu thức 1 + 3 x 2 n là:
A. 61236
B. 256 x 3
C. 252
D. 61236 x 3
Cho hàm số y = ln 2 x - a - 2 m ln 2 x - a + 2 (m là tham số thực), trong đó x, a là các số thực thỏa mãn đẳng thức
log 2 x 2 + a 2 + log 2 x 2 + a 2 + log 2 x 2 + a 2 + . . . + log . . . 2 ⏝ n c ă n x 2 + a 2 - 2 n + 1 - 1 log 2 x a + 1 = 0 (với n là số nguyên dương). Gọi S là tập hợp các giá trị của m thỏa mãn M a x 1 ; e 2 y = 1 . Số phần tử của S là:/
A. 0
B. 1
C. 2
D. Vô số
Cho tập hợp X có n phần tử n ∈ N * , số hoán vị n phần tử của tập hợp X là
A. n!
B. n
C. n 2
D. n 3
Gọi a 2018 là hệ số của số hạng chứa x 2018 trong khai triển nhị thức Niutơn x − x n với x ≥ 0 ; n là số nguyên dương thỏa mãn 1 2 ! .2017 ! + 1 4 ! .2015 ! + 1 6 ! .2013 ! ... + 1 2016 ! .3 ! + 1 2018 ! = 2 2018 − 1 P n . Tìm a 2018
A. 2017
B. − C 2018 3 .
C. 2019
D. C 2019 2 .
Cho A=n-2/n+5 (n là số nguyên,n ko bằng -5).
a, Tìm n để A là số nguyên.
b,Tính giá trị của B=(n+5)^2014+2013 khi A đạt giá trị nhỏ nhất.
Giúp mk nha
Câu 1:
a, Giả sử n là số tự nhiên thỏa mãn điều kiện n(n+1) +6 không chia hết cho 3. Chứng minh rằng 2n^2+n+8 không là số chính phương![]()
b, cho 4 số dương a;b;c;d thỏa mãn điều kiện a^4/b + c^4/d = 1/(b+d) và a^2 + c^2 =1 . Chứng minh rằng (a^2014)/(b^1007) + ( c^ 2014)/(d^1007) =
2/( b+d)^1007 ![]()
![]()
.Mọi người giải giúp Linh nha ^^ Linh đang cần gấp ạ!![]()
![]()
![]()
Tìm số nguyên dương n thỏa mãn các điều kiện sau
C n - 1 4 - C n - 1 3 < 5 4 A n - 2 2 C n + 1 n - 4 ≥ 7 15 A n + 1 3
(Ở đây A n k ; C n k lần lượt là số chỉnh hợp và số tổ hợp chập k của n phần tử).
A. n = 7
B. n = 8
C. n = 9
D. n = 10
1)Cho a,b,c là các số thực thỏa mãn: a+b+c=2015 và \(\frac{1}{a}+\frac{1}{b}+\frac{1}{c}=\frac{1}{2015}\).Tính \(\frac{1}{a^{2015}}+\frac{1}{b^{2015}}+\frac{1}{c^{2015}}\)
2)Cho n là số dương.Chứng minh:
T= \(2^{3n+1}-2^{3n-1}+1\) là hợp số.
3)Cho a,b,c là ba số dương và \(\frac{1}{a}+\frac{1}{b}+\frac{1}{c}=3\).Tìm Max A=\(\frac{1}{\sqrt{a^2-ab+b^2}}+\frac{1}{\sqrt{b^2-bc+c^2}}+\frac{1}{\sqrt{c^2-ac+a^2}}\)