Đáp án A.
Phương trình hoành độ giao điểm là
x4 – 2x2 = x2 – 2 <=> x4 – 3x2 + 2 = 0

Vậy có 4 giao điểm của hai đồ thị.
Đáp án A.
Phương trình hoành độ giao điểm là
x4 – 2x2 = x2 – 2 <=> x4 – 3x2 + 2 = 0

Vậy có 4 giao điểm của hai đồ thị.
Tìm số giao điểm của đồ thị hàm số y = x4 – 2x2 và đồ thị hàm số y = x2 – 2
A. 4
B. 2
C. 3
D. 1
Cho hàm số y = x4 – 4x2 – 2 có đồ thị (C) và đồ thị (P) : y = 1- x2. Số giao điểm của (P) và đồ thị (C) là
A. 2
B. 1
C. 3
D. 4
Gọi M và N là giao điểm của đồ thị hai hàm số y = x 4 - 2 x 2 + 2 và y = - x 2 + 4 . Tọa độ trung điểm I của đoạn thẳng MN là
A. (1;0)
B. (0;2)
C. (2;0)
D. (0;1)
Cho hàm số y = x4 – 2x2 – 1. Tìm số giao điểm của đồ thị hàm số với trục Ox:
A. 1.
B. 3
C. 4
D. 2
Số giao điểm của trục hoành và đồ thị hàm số y = -x4 + 2x2 + 3 là:
A. 1
B. 3
C. 2
D. 4
Cho hàm số y = - x 4 + 2 x 2 - 1 . Số giao điểm của đồ thị hàm số với trục Ox là
A. 1
B. 2
C. 3
D. 4
Cho hàm số: y = x 4 4 - 2 x 2 - 9 4
Biện luận theo k số giao điểm của (C) với đồ thị (P) của hàm số: y = k – 2 x 2
Tìm khẳng định đúng trong các khẳng định sau đây:
A. Hàm số y = x 3 - 5 có hai cực trị;
B. Hàm số y = x 4 /4 + 3 x 2 - 5 luôn đồng biến;
C. Tiệm cận ngang của đồ thị hàm số 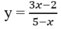 là y = -3;
là y = -3;
D. Đồ thị hàm số sau có hai tiệm cận đứng
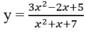
Giả sử đồ thị của hàm số y = x 4 - 2 x 2 - 1 là ( C ) , khi tịnh tiến ( C ) theo O x qua trái 1 đơn vị thì sẽ được đồ thị của một hàm số trong 4 hàm số được liệt kê ở bốn phương án A, B, C, D dưới đây. Hỏi hàm số đó là hàm số nào?
![]()
![]()
![]()
![]()