Đáp án D.
Xét phương trình y = 0
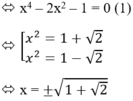
Phương trình (1) có hai nghiệm => số giao điểm của đồ thị với trục Ox là 2
Đáp án D.
Xét phương trình y = 0
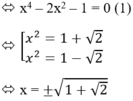
Phương trình (1) có hai nghiệm => số giao điểm của đồ thị với trục Ox là 2
Cho hàm số y = - x 4 + 2 x 2 - 1 . Số giao điểm của đồ thị hàm số với trục Ox là
A. 1
B. 2
C. 3
D. 4
Số giao điểm của trục hoành và đồ thị hàm số y = -x4 + 2x2 + 3 là:
A. 1
B. 3
C. 2
D. 4
Tìm số giao điểm của đồ thị hàm số y = x4 – 2x2 và đồ thị hàm số y = x2 – 2
A. 4
B. 2
C. 3
D. 1
Tìm số giao điểm của đồ thị hàm số y = x4 – 2x2 và đồ thị hàm số y = x2 – 2
A. 4
B. 2.
C. 3
D. 1
Giả sử đồ thị của hàm số y = x 4 - 2 x 2 - 1 là ( C ) , khi tịnh tiến ( C ) theo O x qua trái 1 đơn vị thì sẽ được đồ thị của một hàm số trong 4 hàm số được liệt kê ở bốn phương án A, B, C, D dưới đây. Hỏi hàm số đó là hàm số nào?
![]()
![]()
![]()
![]()
Cho hàm số y = x 4 + 4 x 2 có đồ thị (C). Tìm số giao điểm của đồ thị (C) và trục hoành?
A. 0
B. 3
C. 1
D. 2
Cho hàm số:
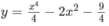
a) Khảo sát sự biến thiên và vẽ đồ thị (C) của hàm số đã cho.
b) Viết phương trình tiếp tuyến của (C) tại các giao điểm của nó với trục Ox.
c) Biện luận theo k số giao điểm của (C) với đồ thị (P) của hàm số: y = k – 2 x 2 .
Cho hàm số y = f(x) = a x + b c x + d ( a,b,c,d ∈ ℝ , - d c ≠ 0) đồ thị hàm số y= f’(x) như hình vẽ.

Biết đồ thị hàm số y= f(x) cắt trục tung tại điểm có tung độ bằng 3. Tìm phương trình tiếp tuyến của (C) tại giao điểm của (C) với trục hoành ?
A. y = x - 3 x + 1
B. y = x + 3 x - 1
C. y = x + 3 x + 1
D. y = x - 3 x - 1
Số giao điểm của đồ thị hàm số y = (x − 3)( x 2 + x + 4) với trục hoành là:
A. 2; B. 3;
C. 0; D. 1.