Các câu hỏi tương tự
cho các số thực x,y,z thỏa mãn \(x^4+y^4+z^4+2x^2y^2z^2=1\). Tìm giá trị nhỏ nhất của biểu thức \(P=x^2+y^2+z^2-\sqrt{2}|xyz|\)
Cho các số thực x,y,z thỏa mãn \(x^4+y^4+z^4+2x^2y^2z^2=1\). Tìm giá trị nhỏ nhất của biểu thức \(P=x^2+y^2+z^2-\sqrt{2}|xyz|\)
cho các số thực x,y,z thỏa mãn x,y,z\(\ge\)1 và \(3\left(x+y+z\right)=x^2+y^2+z^2+2xy\)
Tìm giá trị nhỏ nhất của biểu thức: P=\(\frac{x^2}{\left(x+y\right)^2+x}+\frac{x}{z^2+x}\)
Cho \(x,y,z\ge0\)thỏa mãn x+y+z=1 . Tìm GTLN của \(P=x^2y+y^2z+z^2x\)
Cho 2 số thực không âm x , y thỏa mãn x + y = 1 . Giá trị lớn nhất của 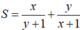 là :
là :
A. 0
B. 1
C. 2
D. 2 3
1) Giải phương trình:
\(4\log_2^2x+x\log_2\left(x+2\right)=2\log_2x\left[x+\log_2\left(x+2\right)\right]\)
2) Tìm tất cả bộ hai số thực \(\left(x;y\right)\) thỏa mãn đẳng thức:
\(x^{\log_2x}+4^y+\left(x-5\right)2^{y+1}+57=18x\)
Giả sử a, b là các số thực sao cho
x
3
+
y
3
a
.
10
3
z
+
b
.
10
2
z
đúng với mọi các số thực dương x, y, z thỏa mãn
log
x
+
y
z...
Đọc tiếp
Giả sử a, b là các số thực sao cho x 3 + y 3 = a . 10 3 z + b . 10 2 z đúng với mọi các số thực dương x, y, z thỏa mãn
log x + y = z và log x 2 + y 2 = z + 1 . Giá trị của a+b bằng
A. - 31 2
B. - 25 2
C. 31 2
D. 29 2
Cho các số nguyên x và y thỏa mãn x + 6y, 5x + 2y, 8x + y theo thứ tự lập thành cấp số cộng; đồng thời
x
+
5
3
,
y
-
1
,
2
x
-
3
y
theo thứ tự lập thành cấp số nhân. Tìm x và y A....
Đọc tiếp
Cho các số nguyên x và y thỏa mãn x + 6y, 5x + 2y, 8x + y theo thứ tự lập thành cấp số cộng; đồng thời x + 5 3 , y - 1 , 2 x - 3 y theo thứ tự lập thành cấp số nhân. Tìm x và y
A. x = 1 y = 3
B. x = 3 y = 1
C. x = - 3 y = - 1
D. x = - 1 y = - 3
Cho các số thực \(x,y,z\in(0;1]\) thỏa mãn \(x+y\ge1+z\). Tìm giá trị nhỏ nhất của biểu thức \(P=\dfrac{x}{y+z}+\dfrac{y}{z+x}+\dfrac{z}{xy+z^2}\)








