Các câu hỏi tương tự
giải phương trình
c)\(\begin{cases} 3x+5y=1\\ 2x-y=-8 \end{cases} \)d)\(\begin{cases} \dfrac{1}{x}-\dfrac{1}{y}=1\\ \dfrac{3}{x}+\dfrac{4}{y}=5 \end{cases} \)
Giải hệ bất phương trình bậc nhất hai ẩn
\(\hept{\begin{cases}y-2>0\\x+1< 0\end{cases}}\)
Giai hệ phương trình sau :
\(\hept{\begin{cases}3^{-x}.2y=1152\\log_{\sqrt{5}}\left(x+y\right)=2\end{cases}}\)
Tí nữa ra đáp án
Giải hệ phương trình: \(\hept{\begin{cases}log_3x+\sqrt{\left(log_3x-1\right)^2+1}=\frac{y}{3}+1\\log_3y+\sqrt{\left(log_3y-1\right)^2+1}=\frac{x}{3}+1\end{cases}}\)
Cho hệ
5
y
+
log
4
x
8
3
5
y...
Đọc tiếp
Cho hệ 5 y + log 4 x = 8 3 5 y . log 4 x = - 1 Gọi x , y là nghiệm của hệ. Tìm x.
![]()
![]()
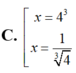
![]()
Trong không gian với hệ trục toạ độ Oxyz, cho đường thẳng d có phương trình:
x
-
12
4
y
-
12
5
z
-
1
4
và mặt phẳng (P): 3x + 5y - z 0. Tìm toạ độ giao điểm của đường thẳng d và mặt phẳng (P). A. (1;0;1) B. (1;1;6) C. (12;0;9) D. (0;0;2)
Đọc tiếp
Trong không gian với hệ trục toạ độ Oxyz, cho đường thẳng d có phương trình: x - 12 4 = y - 12 5 = z - 1 4 và mặt phẳng (P): 3x + 5y - z = 0. Tìm toạ độ giao điểm của đường thẳng d và mặt phẳng (P).
A. (1;0;1)
B. (1;1;6)
C. (12;0;9)
D. (0;0;2)
Cho mặt phẳng (α) có phương trình: 3x + 5y - z - 2 0 và đường thẳng d có phương trình:
x
12
+
4
t
y
9
+
3
t
z...
Đọc tiếp
Cho mặt phẳng (α) có phương trình: 3x + 5y - z - 2 = 0 và đường thẳng d có phương trình: x = 12 + 4 t y = 9 + 3 t z = 1 + t
Tìm giao điểm M của đường thẳng d và mặt phẳng α .
\(\hept{\begin{cases}x^3+y^3=x^2+xy+y^2\\\sqrt{6x^2y^2-x^4-y^4}=\frac{13}{4}\left(x+y\right)-2xy-\frac{3}{4}\end{cases}}\)
Tìm tất cả các giá trị thực của tham số m để hệ phương trình sau có nghiệm
x
2
+
4
x
+
y
m
2...
Đọc tiếp
Tìm tất cả các giá trị thực của tham số m để hệ phương trình sau có nghiệm x 2 + 4 x + y = m 2 x 2 + x y ( x + 2 ) = 9
A. m ≥ 6
B. - 10 ≤ m ≤ 6
C. m ≤ - 10
D. m ≤ - 10 hoặc m ≥ 6







