Chọn C
F ( x ) = ∫ sin 2 x 2 d x = 1 2 ∫ 1 - cos x d x = x 2 - 1 2 sin x + C
F π 2 = π 4 ⇔ π 4 - 1 2 sin π 2 + C ⇔ C = 1 2
Chọn C
F ( x ) = ∫ sin 2 x 2 d x = 1 2 ∫ 1 - cos x d x = x 2 - 1 2 sin x + C
F π 2 = π 4 ⇔ π 4 - 1 2 sin π 2 + C ⇔ C = 1 2
Tìm nguyên hàm F(x) của hàm số f x = sin ( π - 2 x ) thỏa mãn F ( x 2 ) = 1
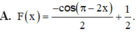
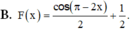
![]()
![]()
Cho f(x)= log 5 ( sin x ) , x ∈ ( 0 ; π / 2 ) . Tính f'(x)
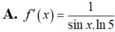
![]()
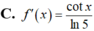
![]()
Tìm hàm số F(x) sao cho F’(x) = f(x) nếu:
f(x) = 1/(cosx)2 với x ∈ ((-π)/2; π/2). f x = 1 cos x 2 v ớ i x ∈ - π 2 ; π 2
Cho hàm số y=f(x) liên tục trên ℝ và có đồ thị như hình bên. Phương trình f( 2 sin x) = m có đúng ba nghiệm phân biệt thuộc đoạn - π ; π khi và chỉ khi
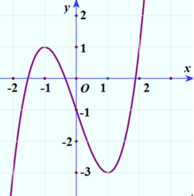
A. m ∈ - 3 ; 1
B. m ∈ - 3 ; 1
C. m ∈ [ - 3 ; 1 )
D. m ∈ ( - 3 ; 1 ]
Biết F(x) là một nguyên hàm của hàm số f x = e - x + sin x thỏa mãn F(0) = 0. Tìm F(x)?
![]()
![]()
![]()
![]()
Tìm giá trị lớn nhất, giá trị nhỏ nhất của các hàm số sau:
a) f(x) = ( 25 - x 2 ) trên đoạn [-4; 4]
b) f(x) = | x 2 – 3x + 2| trên đoạn [-10; 10]
c) f(x) = 1/sinx trên đoạn [π/3; 5π/6]
d) f(x) = 2sinx + sin2x trên đoạn [0; 3π/2]
Biết F(x) là một nguyên hàm của hàm số f(x) = sin x và đồ thị hàm số y = F(x) đi qua điểm M(0;1) . Tính F π 2 .
A. F π 2 = 0
B. F π 2 = 1
C. F π 2 = 2
D. F π 2 = - 1
Giá trị lớn nhất của hàm số f(x) = sin x + cos 2x trên [0; π ] là
A. 5 4
B. 1
C. 2
D. 9 8
Biết F(x) là một nguyên hàm của hàm số f(x) = sin 2x + cosx. Giá trị F π 2 - F ( 0 ) bằng
A. 2.
B. 1.
C. -1.
D. 4.
Cho hàm số f(x) liên tục trên khoảng (-2; 3). Gọi F(x) là một nguyên hàm của f(x) trên khoảng (-2; 3). Tính 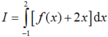 , biết F(-1) = 1, F(2) = 4.
, biết F(-1) = 1, F(2) = 4.
A. I = 6.
B. I = 10.
C. I = 3.
D. I = 9.