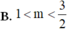Question

Tìm \(m\) để phương trình \(\log_2^2x-2m\log_2x+3m-2=0\) có 2 nghiệm phân biệt \(x_1\), \(x_2\) sao cho \(x_1x_2=2\).

Answer 1

Đặt \(t=\log_2\left(x\right)\Rightarrow\) pt trở thành \(t^2-2mt+3m-2=0\left(1\right)\)

Với mỗi nghiệm t cho một nghiệm x

Để pt đề cho có 2 nghiệm phân biệt thì pt (1) cũng có 2 nghiệm phân biệt

\(\Delta'=m^2-3m+2>0\Rightarrow\left[{}\begin{matrix}m>2\\m< 1\end{matrix}\right.\)

\(x_1x_2=2\Rightarrow\log_2\left(x_1x_2\right)=1\Rightarrow\log_2\left(x_1\right)+\log_2\left(x_2\right)=1\Rightarrow t_1+t_2=1\)

Áp dụng định lý Vi-ét \(\Rightarrow2m=1\Rightarrow m=\dfrac{1}{2}\) (thỏa điều kiện denta phẩy)