- Ta có:
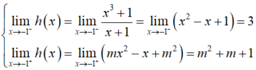
- Hàm số có giới hạn tại x = -1 khi và chỉ khi:
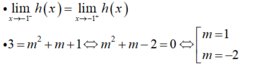
- Vậy để hàm số đã cho có giới hạn tại x = -1 khi m = 1 hoặc m = -2.
- Ta có:
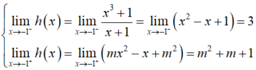
- Hàm số có giới hạn tại x = -1 khi và chỉ khi:
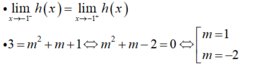
- Vậy để hàm số đã cho có giới hạn tại x = -1 khi m = 1 hoặc m = -2.
tìm m để hàm số \(f\left(x\right)=\left\{{}\begin{matrix}\dfrac{\sqrt{2x+7}-\sqrt{x+3}-5}{x-1}\Leftrightarrow x>1\\2x+m\Leftrightarrow x\le1\end{matrix}\right.\) có giới hạn tại \(x_0=1\)
Tìm các giá trị thực của tham số m để hàm số h x = x 3 + 1 x + 1 k h i x < - 1 m x 2 - x + m 2 k h i x ≥ - 1 để hàm số có giới hạn tại x= -1.
A. m = -1; m = 2.
B.m = -1; m = -2.
C. m=1; m = -2.
D. m=1;m= 2
Tìm các giá trị thực của tham số m để hàm số f x = x + m k h i x < 0 x 2 + 1 k h i x ≥ 0 có giới hạn tại x= 0.
A. m= -1
B. m= 2
C. m= -2
D. m =1
Tìm m để hàm số sau có giới hạn khi x → 1: f x = x 2 + x - 2 1 - x + m x + 1 k h i x < 1 3 m x + 2 m - 1 k h i x ≥ 1
A. m = 2 3
B. m = 2 5
C. m = 3 2
D. m = 1 2
Tìm m để hàm số sau có giới hạn khi x → 1.
f x = x 2 + x - 2 1 - x + m x + 1 k h i x < 1 3 m x + 2 m - 1 k h i x ≥ 1
A. 2 3
B. 2 5
C. 3 2
D. 1 2
Tìm m để các hàm số f ( x ) = x 2 + m x + 2 m + 1 x + 1 k h i x ≥ 0 2 x + 3 m - 1 1 - x + 2 k h i x < 0 có giới hạn khi x → 1
Tìm a để hàm số f ( x ) = 5 a x 2 + 3 x + 2 a + 1 k h i x ≥ 0 1 + x + x 2 + x + 2 k h i x < 0 có giới hạn tại x → 0
A. +∞
B. -∞
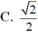
D. 1
Tìm a để hàm số f ( x ) = x 2 + a x + 2 , x > 1 2 x 2 - x + 3 a , x ≤ 1 có giới hạn khi x → 1.
A. 2
B. 3
C. -1
D. 1
Cho hàm số f ( x ) = ( x + 1 ) 2 , x > 1 x 2 + 3 , x < 1 k 2 , x = 1 . Tìm k để f(x) gián đoạn tại x = 1.
A. k ≠ ±2.
B. k ≠ 2.
C. k ≠ -2.
D. k ≠ ±1.