Các câu hỏi tương tự
Tìm các giá trị của tham số m để đồ thị hàm số y =mx^4 +(2m-1)x^2 +m -2 chỉ có 1 cực đại và ko có cực tiểu.
Tìm tất cả các giá trị thực của tham số m để điểm M( 2m3; m) tạo với hai điểm cực đại, cực tiểu của đồ thị hàm số y 2x3-3( 2m+ 1) x2+ 6m( m+1) x+1 (C) một tam giác có diện tích nhỏ nhất. A. -1 B. 0 C. 1 D. 2
Đọc tiếp
Tìm tất cả các giá trị thực của tham số m để điểm M( 2m3; m) tạo với hai điểm cực đại, cực tiểu của đồ thị hàm số y= 2x3-3( 2m+ 1) x2+ 6m( m+1) x+1 (C) một tam giác có diện tích nhỏ nhất.
A. -1
B. 0
C. 1
D. 2
Cho hàm số y f(x) -x3 + (2m – 1)x2 – (2 – m)x – 2. Tìm m để đồ thị hàm số có cực đại và cực tiểu? A. m ∈ (-1; +∞) B. m ∈ (-1; 5/4) C. m ∈ (-∞; -1) D. m ∈ (-∞; -1) ∪ (5/4; +∞)
Đọc tiếp
Cho hàm số y = f(x) = -x3 + (2m – 1)x2 – (2 – m)x – 2. Tìm m để đồ thị hàm số có cực đại và cực tiểu?
A. m ∈ (-1; +∞)
B. m ∈ (-1; 5/4)
C. m ∈ (-∞; -1)
D. m ∈ (-∞; -1) ∪ (5/4; +∞)
Tìm các giá trị của m để đồ thị hàm số y(x+1)(x-2)(x-m) có hai điểm cực trị thuộc về hai phía Ox.
Đọc tiếp
Tìm các giá trị của m để đồ thị hàm số y=(x+1)(x-2)(x-m) có hai điểm cực trị thuộc về hai phía Ox.
![]()
![]()
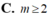
![]()
Tìm điều kiện của m để đồ thị
(
C
)
:
y
m
x
4
-
(
m
2
-
1
)
x
2
-
1
có hai điểm cực đại.
Đọc tiếp
Tìm điều kiện của m để đồ thị ( C ) : y = m x 4 - ( m 2 - 1 ) x 2 - 1 có hai điểm cực đại.
![]()
![]()
![]()
![]()
Cho hàm số yx4-2( m2-m+1)x2+m-1 với m là tham số thực. Tìm giá trị của m để đồ thị hàm số có một điểm cực đại và hai điểm cực tiểu, đồng thời khoảng cách giữa hai điểm cực tiểu ngắn nhất. A. m -1/2 B. m 1/2 C. m2 D. m1
Đọc tiếp
Cho hàm số y=x4-2( m2-m+1)x2+m-1 với m là tham số thực. Tìm giá trị của m để đồ thị hàm số có một điểm cực đại và hai điểm cực tiểu, đồng thời khoảng cách giữa hai điểm cực tiểu ngắn nhất.
A. m= -1/2
B. m= 1/2
C. m=2
D. m=1
Tìm tất cả các giá trị thực của tham số m để điểm
M
(
2
m
3
;
m
)
tạo với hai điểm cực đại, cực tiểu của đồ thị hàm số
y
2
x
3
-
3
(...
Đọc tiếp
Tìm tất cả các giá trị thực của tham số m để điểm M ( 2 m 3 ; m ) tạo với hai điểm cực đại, cực tiểu của đồ thị hàm số y = 2 x 3 - 3 ( 2 m + 1 ) x 2 + 6 m ( m + 1 ) x + 1 một tam giác có diện tích nhỏ nhất
A. m = 2
B. m = 0
C. m = 1
D. m = -1
Tìm tất cả các giá trị thực của tham số m để hàm số
y
x
3
-
3
m
x
2
+
(
m
-
1
)
x
+
2
có cực đại, cực tiểu và các đ...
Đọc tiếp
Tìm tất cả các giá trị thực của tham số m để hàm số y = x 3 - 3 m x 2 + ( m - 1 ) x + 2 có cực đại, cực tiểu và các điểm cực trị của đồ thị hàm số có hoành độ dương
A. 0 ≤ m ≤ 1
B. m ≥ 1
C. m ≥ 0
D. m > 1
Tìm các giá trị của tham số m để đồ thị hàm số:
y
x
3
-
3
x
2
-
m
x
+
2
có điểm cực đại và điểm cực tiểu cách đều đường thẳng có phương trình:
y...
Đọc tiếp
Tìm các giá trị của tham số m để đồ thị hàm số: y = x 3 - 3 x 2 - m x + 2 có điểm cực đại và điểm cực tiểu cách đều đường thẳng có phương trình: y = x - 1 ( d )
A. m = 0
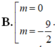
C. m = 2
D. m = - 9 2