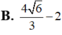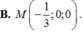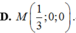Câu 1: Cho đường thẳng (d) xác định bởi hept{begin{cases}y-1x+z0end{cases}}và hai mặt phẳng (P): x+2y+2z+30,(Q): x+2y+2z+70.(Chọn đáp án đúng) Phương trình mặt cầu có tâm thuộc (d) và tiếp xúc với (P), (Q) là:a)left(x+3right)^2+left(y+1right)^2+left(z+3right)^2frac{4}{9}b)left(x+3right)^2+left(y+1right)^2+left(z-3right)^2frac{4}{9}c)left(x-3right)^2+left(y+1right)^2+left(z+3right)^2frac{4}{9}d)left(x-3right)^2+left(y-1right)^2+left(z+3right)^2frac{4}{9}Câu 2: Cho mặt cầu (S): x^2+y^2+z^2-2x+2y+1...
Đọc tiếp
Câu 1: Cho đường thẳng (d) xác định bởi \(\hept{\begin{cases}y=-1\\x+z=0\end{cases}}\)và hai mặt phẳng (P): \(x+2y+2z+3=0,\)(Q): \(x+2y+2z+7=0\).
(Chọn đáp án đúng) Phương trình mặt cầu có tâm thuộc (d) và tiếp xúc với (P), (Q) là:
\(a)\left(x+3\right)^2+\left(y+1\right)^2+\left(z+3\right)^2=\frac{4}{9}\)
\(b)\left(x+3\right)^2+\left(y+1\right)^2+\left(z-3\right)^2=\frac{4}{9}\)
\(c)\left(x-3\right)^2+\left(y+1\right)^2+\left(z+3\right)^2=\frac{4}{9}\)
\(d)\left(x-3\right)^2+\left(y-1\right)^2+\left(z+3\right)^2=\frac{4}{9}\)
Câu 2: Cho mặt cầu (S): \(x^2+y^2+z^2-2x+2y+1=0\)và điểm \(M\left(0;-1;0\right).\)
Phương trình mặt phẳng (P) tiếp xúc với (S) tại M là:
\(a)2x+y-z+1=0.\) \(b)x=0.\)
\(c)-x+y+2z+1=0.\) \(d)x+y+1=0\)
Câu 3: Trong khai triển \(f\left(x\right)=\frac{1}{256}\left(2x+3\right)^{10}\)thành đa thức, hệ số của x8 là:
\(a)103680.\) \(b)405.\) \(c)106380.\) \(d)504.\)
Câu 4: Tổng các nghiệm của phương trình \(2^{x^2-3}.5^{x^2-3}=0,01.\left(10^{x-1}\right)^3\)là:
\(a)3.\) \(b)5.\) \(c)0.\) \(d)2\sqrt{2}.\)