Đáp án C
Phương pháp:
Phân tích đa thức 1 + x + x 2 + x 3 thành nhân tử.
Sử dụng khai triển nhị thức Newton:
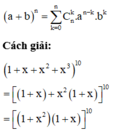
Áp dụng khai triển nhị thức Newton ta có:
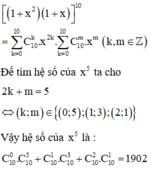
Đáp án C
Phương pháp:
Phân tích đa thức 1 + x + x 2 + x 3 thành nhân tử.
Sử dụng khai triển nhị thức Newton:
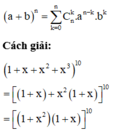
Áp dụng khai triển nhị thức Newton ta có:
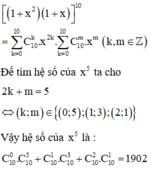
Trong khai triển nhị thức ( x + 1 x ) n hệ số của số hạng thứ 3 lớn hơn hệ số của số hạng thứ 2 là 35. Tìm số hạng không chứa x trong khai triển nói trên.
A. 225
B. 252
C. 522
D. 525
Tìm hệ số của x5 trong khai triển P(x)=(1+x)+2(1+x)2+ … + 8(1+x)8
A. 630
B. 635
C. 636
D. 637
Tìm hệ số của số hạng chứa x 5 trong khai triển ( 1 + x + x 2 + x 3 ) 10 .
A. 582
B. 1902
C. 7752
D. 252
Cho biết 3 số hạng đầu của khai triển ( x + 1 2 x ) n , x > 0 có các hệ số là 3 số hạng liên tiếp của một cấp số cộng. Tìm số hạng thứ 5 trong khai triển trên
A. 35 8 x 4
B. 35 8
C. 53 8 x 4
D. 53 8
Tìm hệ số của x 4 trong khai triển P ( x ) = ( 1 - x - 3 x 3 ) n với n là số tự nhiên thỏa mãn hệ thức C n n - 2 + 6 n + 5 = A n + 1 2
A. 210
B. 840
C. 480
D. 270
Hệ số của x 5 trong khai triển x ( 1 - 2 x ) 5 + x 2 ( 1 + 3 x ) 10 là:
A. 61204
B. 3160
C. 3320
D. 61268
Tìm hệ số của x 5 trong khai triển P(x)= ( x + 1 ) 6 + ( x + 1 ) 7 + . . . + ( x + 1 ) 12
A. 1715
B. 1711
C. 1287
D. 1716
Tìm hệ số của x 7 trong khai triển P ( x ) = ( x + 1 ) 20
A. C 20 7
B. A 20 7
C. A 20 13
D. P 7
Cho biết 3 số hạng đầu của khai triển x + 1 2 x n có các hệ số là 3 số hạng liên tiếp của một cấp số cộng. Tìm số hạng thứ 5 trong khai triển trên.
A. 35 4 x 4
B. 35 8
C. 53 8 x 4
D. 53 8
Cho khai triển x + 2 x 6 với x > 0 . Tìm hệ số của số hạng chứa x 3 trong khai triển trên.
A. 80
B. 160
C. 240
D. 60