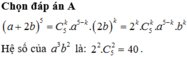Các câu hỏi tương tự
Trong khai triển nhị thức ( x + 1 x ) n hệ số của số hạng thứ 3 lớn hơn hệ số của số hạng thứ 2 là 35. Tìm số hạng không chứa x trong khai triển nói trên.
A. 225
B. 252
C. 522
D. 525
Cho khai triển nhị thức:
a
b
3
+
b
2
b
2
3
a...
Đọc tiếp
Cho khai triển nhị thức: a b 3 + b 2 b 2 3 a a 2 3 3 n với
a ≠ 0 ; b ≠ 0 . Hãy xác định hệ số của số hạng có tỉ số lũy thừa của a và b bằng - 1 2 biết rằng
3 C 24 0 - 1 2 C 2 n 1 + C 2 n 2 - 1 4 C 2 n 3 + . . . + 3 2 n + 1 C 2 n 2 n = 10923 5
A. 161280
B. 280161
C. 280116
D, 116280
Tìm hệ số của
x
10
trong khai triển nhị thức Niu Tơn
2
+
x
n
, biết rằng
C
n
0
.3
n
−
C
n
1
.3
n
−
1
+...
Đọc tiếp
Tìm hệ số của x 10 trong khai triển nhị thức Niu Tơn 2 + x n , biết rằng C n 0 .3 n − C n 1 .3 n − 1 + C n 2 .3 n − 2 − C n 3 .3 n − 3 + ... + − 1 n C n n = 2048
A. 12
B. 21
C. 22
D. 23
Tìm hệ số của số hạng chứa x 9 trong khai triển nhị thức Newton của biểu thức 3 + x 11
A. 9
B. 110
C. 495
D. 55
Gọi a là hệ số không chứa x trong khai triển khai triển nhị thức Niu-tơn
x
2
−
2
x
n
C
n
0
x
2
n
+
C
n...
Đọc tiếp
Gọi a là hệ số không chứa x trong khai triển khai triển nhị thức Niu-tơn x 2 − 2 x n = C n 0 x 2 n + C n 1 x 2 n − 1 − 2 x + … + C n n − 1 x 2 − 2 x n − 1 + C n n − 2 x n (n là số nguyên dương).
Biết rằng trong khai triển trên tổng hệ số của ba số hạng đầu bằng 161. Tìm a
A. a = 11520
B. a = 11250
C. a = 12150
D. a = 10125
Gọi a là hệ số không chứa x trong khai triển nhị thức Niu – tơn:
x
2
−
2
x
n
C
n
0
x
2
n
+
C
n
1...
Đọc tiếp
Gọi a là hệ số không chứa x trong khai triển nhị thức Niu – tơn:
x 2 − 2 x n = C n 0 x 2 n + C n 1 x 2 n − 1 − 2 x + ... + C n n − 1 x 2 − 2 x n − 1 + C n n − 2 x n n ∈ ℕ * .
Biết rằng trong khai triển trên tổng hệ số của ba số hạng đầu bằng 161. Tìm a
A. a = 11520
B. a =11250
C. a = 12150
D. a = 10125
Hệ số của trong khai triển của nhị thức Niu tơn
(
3
-
x
)
9
là A.
-
C
9
7
B.
C
9
7
C.
9
C...
Đọc tiếp
Hệ số của trong khai triển của nhị thức Niu tơn ( 3 - x ) 9 là
A. - C 9 7
B. C 9 7
C. 9 C 9 7
D. - 9 C 9 7
Biết rằng hệ số của
x
4
trong khai triển nhị thức Newton
2
−
x
n
,
n
∈
ℕ
*
bằng 280. Tìm n. A. n8 B. n6 C. n7 D. n5
Đọc tiếp
Biết rằng hệ số của x 4 trong khai triển nhị thức Newton 2 − x n , n ∈ ℕ * bằng 280. Tìm n.
A. n=8
B. n=6
C. n=7
D. n=5
Tìm hệ số của
x
10
trong khai triển nhị thức Niu Tơn
(
2
+
x
)
n
, biết rằng
C
n
0
.
3
n
-
C
n
1
.
3
n
-...
Đọc tiếp
Tìm hệ số của x 10 trong khai triển nhị thức Niu Tơn ( 2 + x ) n , biết rằng C n 0 . 3 n - C n 1 . 3 n - 1 + C n 2 . 3 n - 2 + . . . + ( - 1 ) C n n = 2048
A. 12
B. 21
C. 22
D. 23