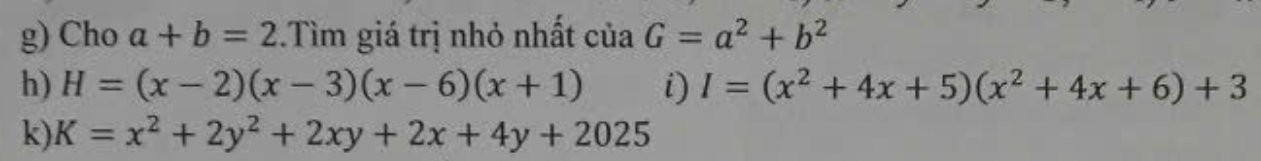`i)`
\(I=\left(x^2+4x+5\right)\left(x^2+4x+6\right)+3\\ =\left(x^2+4x+5\right)\left(x^2+4x+5+1\right)+3\\ =\left(x^2+4x+5\right)^2+\left(x^2+4x+5\right)+3\\ =\left(x^2+4x+5\right)^2+\left(x^2+4x+4\right)+1+3\\ =\left(x^2+4x+5\right)^2+\left(x+2\right)^2+4\)
Có `x^2+4x+5=x^2+4x+4+1`
hay `x^2+4x+5=(x+2)^2+1`
mà `(x+2)^2>=0 AA x => (x+2)^2+1>=1`
hay `x^2+4x+5>=1`
`AA x` ta có :`{:((x^2+4x+5)^2>=1),((x+2)^2>=0):}}`
`=>(x^2+4x+5)^2+(x+2)^2>=0+1`
`=>(x^2+4x+5)^2+(x+2)^2+4>=1+4`
hay `I>=5`
Dấu `"="` xảy ra khi \(\left\{{}\begin{matrix}\left(x^2+4x+5\right)^2=1\\\left(x+2\right)^2=0\end{matrix}\right.\\ \Rightarrow\left\{{}\begin{matrix}x^2+4x+5=1\left(x^2+4x+5>0\right)\\x+2=0\end{matrix}\right.\\ \Rightarrow\left\{{}\begin{matrix}x^2+4x+4=0\\x=-2\end{matrix}\right.\\ \Rightarrow\left\{{}\begin{matrix}\left(x+2\right)^2=0\\x=-2\end{matrix}\right.\Rightarrow x=-2\)
Vậy `Mi n I=5` khi `x=-2`