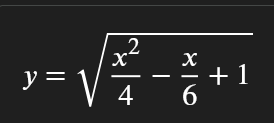Ta có:
\(y=\sqrt{\dfrac{x^2}{4}-\dfrac{x}{6}+1}\\ =\sqrt{\left(\dfrac{x}{2}\right)^2-2\cdot\dfrac{x}{2}\cdot\dfrac{1}{6}+\left(\dfrac{1}{6}\right)^2+\dfrac{35}{36}}\\ =\sqrt{\left(\dfrac{x}{2}-\dfrac{1}{6}\right)^2+\dfrac{35}{36}}\)
Ta có:
\(\left(\dfrac{x}{2}-\dfrac{1}{6}\right)^2\ge0\forall x=>y=\sqrt{\left(\dfrac{x}{2}-\dfrac{1}{6}\right)^2+\dfrac{35}{36}}\ge\sqrt{0+\dfrac{35}{36}}=\dfrac{\sqrt{35}}{6}\)
Dấu "=" xảy ra: \(\dfrac{x}{2}-\dfrac{1}{6}=0< =>x=\dfrac{1}{3}\)
Đúng 3
Bình luận (0)
