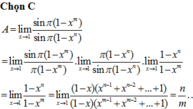Các câu hỏi tương tự
Tập nghiệm của phương trình sin(πx) = cos(π/3+πx) là
A. {π/12+kπ,k∈Z}
B. {1/12+k,k∈Z}
C. {π/2+kπ,k∈Z}
D. {1/2+kπ,k∈Z}
Tìm giới hạn
F
lim
x
→
+
∞
3
sin
x
+
2
cos
x
x
+...
Đọc tiếp
Tìm giới hạn F = lim x → + ∞ 3 sin x + 2 cos x x + 1 + x :
A. +∞
B. -∞
C. 5/2
D. 0
Tìm giới hạn
A
lim
x
→
0
1
+
sin
m
x
-
cos
m
x
1
+
sin
n...
Đọc tiếp
Tìm giới hạn A = lim x → 0 1 + sin m x - cos m x 1 + sin n x - cos n x
A. +∞
B. -∞
C. m/n
D. 0
Tìm giới hạn
A
lim
x
→
0
1
+
sin
m
x
-
cos
m
x
1
+
sin...
Đọc tiếp
Tìm giới hạn A = lim x → 0 1 + sin m x - cos m x 1 + sin n x - cos n x .
![]()
![]()
![]()
![]()
Tìm giới hạn
A
lim
x
→
0
1
-
cos
2
x
2
sin
3
x
2
. A.
+
∞
B. ...
Đọc tiếp
Tìm giới hạn A = lim x → 0 1 - cos 2 x 2 sin 3 x 2 .
A. + ∞
B. - ∞
C. 1
D. 0
Tìm giới hạn
B
lim
x
→
0
cos
2
x
-
cos
3
x
x
(
sin
3
x
-...
Đọc tiếp
Tìm giới hạn B = lim x → 0 cos 2 x - cos 3 x x ( sin 3 x - sin 4 x )
A. +∞
B. -∞
C. 5/2
D. 0
Tìm các giới hạn sau:
1/ \(\lim\limits_{x->-1}\) \(\dfrac{x^{2019}+1}{x^2+x}\)
2/ \(\lim\limits_{x->1}\) \(\dfrac{x+x^2+...+x^n-n}{x-1}\)
Tìm khẳng định đúng trong các khẳng định sau:
(
I
)
f
(
x
)
1
x
2
-
1
liên tục với mọi x.
(
II
)
f
(
x
)
sin
x
...
Đọc tiếp
Tìm khẳng định đúng trong các khẳng định sau:
( I ) f ( x ) = 1 x 2 - 1 liên tục với mọi x.
( II ) f ( x ) = sin x x có giới hạn khi x → 0.
( III ) f ( x ) = 9 - x 2 liên tục trên đoạn [-3; 3].
A. Chỉ (I) và (II).
B. Chỉ (II) và (III).
C. Chỉ (II).
D. Chỉ (III).
1) Tính giới hạn \(\lim\limits_{n\rightarrow\infty}\dfrac{-n^2+2n+1}{\sqrt{3n^4+2}}\)
2) Tính giới hạn \(\lim\limits_{n\rightarrow\infty}\left(\dfrac{4n-\sqrt{16n^2+1}}{n+1}\right)\)
3) Tính giới hạn \(\lim\limits_{n\rightarrow\infty}\left(\dfrac{\sqrt{9n^2+n+1}-3n}{2n}\right)\)