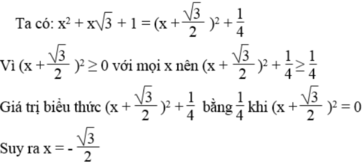Các câu hỏi tương tự
Tìm giá trị nhỏ nhất của biểu thức sau. Giá trị đó đạt được khi x bằng bao nhiêu ? \(x^2+x\sqrt{3}+1\)
a) Chứng minh: \(x^2+x\sqrt{3}+1=\left(x+\frac{\sqrt{3}}{2}\right)^2+\frac{1}{4}\)
b) Tìm giá trị nhỏ nhất của biểu thức \(x^2+x\sqrt{3}+1\) Giá trị đó đạt được khi x bằng bao nhiêu ?
Chứng minh:
x
-
x
+
1
x
-
1
2
2
+
3
4
với x 0. Từ đó, cho biết...
Đọc tiếp
Chứng minh: x - x + 1 = x - 1 2 2 + 3 4 với x > 0. Từ đó, cho biết biểu thức 1 x - x + 1 có giá trị lớn nhất là bao nhiêu? Giá trị đó đạt được khi x bằng bao nhiêu?
cho A=\(\sqrt{x^2+2x+1}+\sqrt{x^2-2x+1}\)
tìm giá trị nhỏ nhất của A, giá trị đó đạt được khi x bằng bao nhiêu?
Cho biểu thức M= x-3/căn(x-1) -căn (2)
tìm giá trị của x để M đạt giá trị nhỏ nhất và tìm giá trị nhỏ nhất đó
cho A = \(\dfrac{1}{x-4\sqrt{x-4}+3}\).Tìm giá trị lớn nhất của A,giá trị đó đạt được khi x bằng bao nhiêu
Cho A=\(\frac{1}{x-2\sqrt{x-5}+3}\)
Tìm giá trị lớn nhất của A, giá trị đó đạt được khi x bằng bao nhiêu
\(A=\sqrt{x^2+2x+1}+\sqrt{x^2-2x+1}\)
Tìm giá trị nhỏ nhất của A, giá trị đó đạt được khi x bằng bao nhiêu?
Cho A= x-\(2\sqrt{x}\)+4 . Tìm giá trị nhỏ nhất của A
Gía trị đó đạt được khi x bằng bao nhiêu?