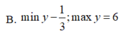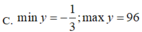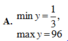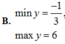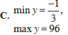Question

tìm giá trị lớn nhất giá trị nhỏ nhất

a) \(y=x^3-3x-4\) trên [-3;2)

b) \(y=\dfrac{3x^2-4x}{x^2-1}\) trên (\(-1;+\infty\))

Answer 1

a.

\(y'=3x^2-3=0\Rightarrow x=\pm1\)

\(y\left(-3\right)=-22;y\left(-1\right)=-2;y\left(1\right)=-6;y\left(2\right)=-2\)

\(\Rightarrow y_{min}=y\left(-3\right)=-22\)

\(y_{max}=y\left(2\right)=y\left(-1\right)=-2\)

b.

\(y'=\dfrac{\left(6x-4\right)\left(x^2-1\right)-2x\left(3x^2-4x\right)}{\left(x^2-1\right)^2}=\dfrac{4x^2-6x+4}{\left(x^2-1\right)^2}=\dfrac{4\left(x-\dfrac{3}{4}\right)^2+\dfrac{7}{4}}{\left(x^2-1\right)^2}>0;\forall x\)

\(\Rightarrow\) Hàm đồng biến trên khoảng đã cho

\(\Rightarrow\) Không tồn tại GTNN và GTLN của hàm số trên khoảng đã cho