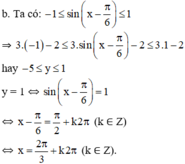
Vậy giá trị lớn nhất của hàm số đạt được là 1 khi
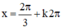 (k ∈ Z).
(k ∈ Z).
Tuyển Cộng tác viên Hoc24 nhiệm kì 26 tại đây: https://forms.gle/dK3zGK3LHFrgvTkJ6
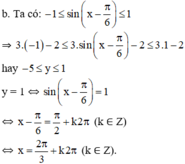
Vậy giá trị lớn nhất của hàm số đạt được là 1 khi
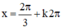 (k ∈ Z).
(k ∈ Z).
Tìm giá trị lớn nhất và giá trị nhỏ nhất của các hàm số :
a. y=\(\sqrt{\text{3(1+ sin(x))}}\)-5
b. y= 6 sin(x+8)-5
Tìm tập giá trị lớn nhất, giá trị nhỏ nhất của hàm số sau y = sin x + 3
![]()
![]()
![]()
![]()
Gọi M và m lần lượt là giá trị lớn nhất và giá trị nhỏ nhất của hàm số y = 2 sin x + cos 2x trên đoạn 0 , π . Khi đó 2M + m bằng
A. 4
B. 5/2
C. 7/2
D. 5
Tìm giá trị lớn nhất của hàm số sau y = sinx - 1 sinx trong khoảng 0 < x < π
A: -1
B: 0
C: 1
D: 2
tìm giá trị lớn nhất và giá trị nhỏ nhất của các hàm số
A. y =\(\sqrt{\text{6(1 + sin(x))}}-9\)
B.y = 4 sin(x+1)−7
Tìm giá trị lớn nhất của hàm số y = x + sin 2 x trên đoạn 0 , π
A. 0
B. π
C . 3 π 4 + 1 2
D . 3 π 4
Tìm giá trị lớn nhất, giá trị nhỏ nhất của hàm số y = 1 - 8sin^2x cos^2x + 2 sin^4 2x
tìm giá trị lớn nhất, giá trị nhỏ nhất của hàm số
a) \(y=cos^23x+9\)
b) \(y=sin^2x-3\)
c) \(y=sin^25x+12\)
Gọi M, m lần lượt là giá trị lớn nhất, giá trị nhỏ nhất của hàm số y = cos x + 2 . sin x + 3 2 . cos x - sin x + 4 . Tính M,m
A. 4/11
B. 3/4
C. 1/2
D. 20/11
Giá trị nhỏ nhất m và giá trị lớn nhất M của hàm số y = sin x + 2 cos x + 1 sin x + cos x + 2 là
![]()
![]()
![]()
![]()