Đáp án C
Ta có f ' x = 3 x 2 − 3 = 0 ⇔ x = ± 1. Mà f − 1 = 4 , f 1 = 0 ; f 2 = 4 ⇒ max − 1 ; 2 f x = 4
Đáp án C
Ta có f ' x = 3 x 2 − 3 = 0 ⇔ x = ± 1. Mà f − 1 = 4 , f 1 = 0 ; f 2 = 4 ⇒ max − 1 ; 2 f x = 4
Cho hàm số y = f(x) xác định trên ℝ và có đồ thị của hàm số f ' ( x ) , biết f ( 3 ) + f ( 2 ) = f ( 0 ) + f ( 1 ) và các khẳng định sau:
Hàm số y = f(x) có 2 điểm cực trị.
Hàm số y = f(x) đồng biến trên khoảng ( - ∞ ; 0 ) .
Max [ 0 ; 3 ] f ( x ) = f ( 3 ) .
Min ℝ f ( x ) = f ( 2 ) .
Max [ - ∞ ; 2 ] f ( x ) = f ( 0 ) .

Số khẳng định đúng là
A. 2.
B. 3.
C. 4.
C. 4.
Cho bài toán: “Tìm Giá trị lớn nhất, giá tri nhỏ nhất của hàm số y = f ( x ) = x + 1 x - 1 trên - 2 ; 3 2 ?”. Một học sinh giải như sau:
Bước 1: y ' = 1 - 1 ( x - 1 ) 2 ∀ x ≢ 1
Bước 2: y ' = 0 ⇔ x = 2 ( L ) x = 0
Bước 3: f ( - 2 ) = - 7 3 ; f ( 0 ) = - 1 ; f 3 2 = 7 2 Vậy m a x [ - 2 ; 3 2 ] f ( x ) = 7 3 ; m i n [ - 2 ; 3 2 ] = - 7 3
Lời giải trên đúng hay sai ? Nêu sai thì sai lừ bưóc nào ?
A. Lời giải trên hoàn toàn đúng
B. Lời giải trên sai từ bước 1
C. Lời giải trên sai từ bước 2
D. Lời giải trên sai từ bước 3
Cho hàm số y=f(x) xác định trên ℝ và có đồ thị của hàm số f'(x), biết f(3)+f(20=f(0)+f(1) và các khẳng định sau:
1) Hàm số y=f(x) có 2 điểm cực trị
2) Hàm số y=f(x) đồng biến trên khoảng - ∞ ; 0
3) M a x 0 ; 3 f x = f 3
4) M a x ℝ f x = f 2
5) M a x - ∞ ; 2 f x = f 0 .
Số khẳng định đúng là

A. 2
B. 3
C. 4
D. 5
Cho đồ thị y=f’(x) trên [m;n] (như hình vẽ). Biết f(a)> f(c)>0; f(d)<f(b)<0 và
m
a
x
f
(
x
)
[
m
;
n
]
=
f
(
n
)
;
m
i
n
f
(
x
)
[
m
;
n
]
=
f
(
m
)
Số điểm cực trị của hàm số
y
=
f
(
x
)
trên [m;n] là
A. 6
B. 8
C. 9
D. 10
Cho hàm số f(x) xác định trên R\{-1;2} thỏa mãn f ' ( x ) = 3 x 2 - x - 2 , f(-2)=2 ln2+2 và f(0)=ln2-1. Giá trị của biểu thức f(-3)+f( 1 2 ) bằng
A. 2+ln5.
B. 2+ln 5 2 .
C. 2-ln2.
D. 1+ln 5 2 .
Cho hàm số y=f(x) liên tục, không âm trên R thỏa mãn f ( x ) . f ' ( x ) = 2 x f ( x ) 2 + 1 và f(0)=0. Giá trị lớn nhất M và giá trị nhỏ nhất m của hàm số y=f(x) trên đoạn [1;3] lần lượt là:
A. M=20;m=2
B. M = 4 11 ; m = 3
C. M = 20 ; m = 2
D. M = 3 11 ; m = 3
Cho các mệnh đề :
1) Hàm số y=f(x) có đạo hàm tại điểm x 0 thì nó liến tục tại x 0 .
2) Hàm số y=f(x) liên tục tại x 0 thì nó có đạo hàm tại điểm x 0 .
3) Hàm số y=f(x) liên tục trên đoạn [a;b] và f(a).f(b)<0 thì phương trình f(x) có ít nhất một nghiệm trên khoảng (a;b).
4) Hàm số y=f(x) xác định trên đoạn [a;b] thì luôn tồn tại giá trị lớn nhất và giá trị nhỏ nhất trên đoạn đó.
Số mệnh đề đúng là:
A. 2
B. 4
C. 3
D. 1
Cho hàm số bậc 3:y=f(x) có đồ thị như hình vẽ.
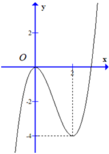
Xét hàm số g(x)=f[(x)]. Trong các mệnh đề dưới đây:
g(x) đồng biến trên (-∞;0) và (2;+∞).
Hàm số g(x) có bốn điểm cực trị.
m a x - 1 ; 1 g x = 0 .
Phương trình g(x)=0 có ba nghiệm.
Số mệnh đề đúng là
A. 3.
B. 2.
C. 1.
D. 4.
Cho hàm số f ( x ) = a x 4 + b x 2 + c có m i n ( - ∞ ; 0 ) f ( x ) = f ( - 1 ) . Giá trị nhỏ nhất của hàm số y=f(x) trên đoạn [ 1 2 ;2] bằng
A. c + 8a
B. c - 7 16 a
C. c + 9 16 a
D. c - a
Cho hàm số f x = a x + b c x + d với a , b , c , d ∈ R có đồ thị hàm số y=f'(x) như hình vẽ bên. Biết rằng giá trị lớn nhất của hàm số y=f(x) trên đoạn [-3;-2] bằng 8. Giá trị của f(2) bằng.

A. 2
B. 5
C. 4
D. 6