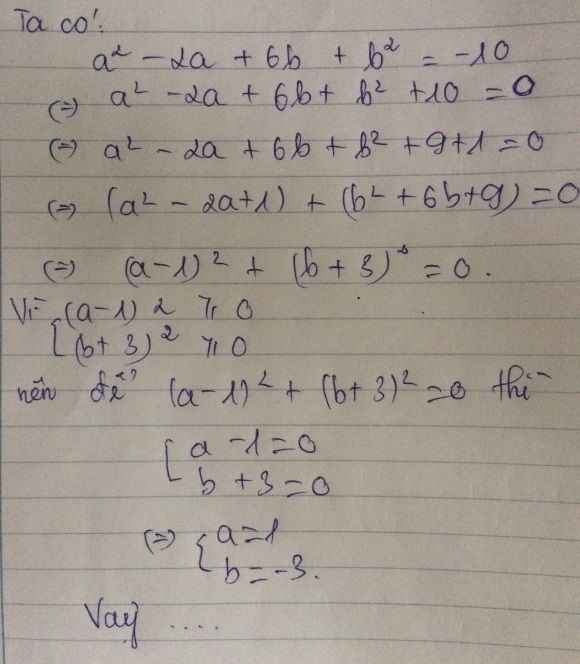a2-2a+6b+b2=-10
⇒ a2-2a+6b+b2+10=0
⇒ (a2-2a+1)+(b2+6b+9)=0
⇒ (a-1)2+(b+3)2=0
vì (a-1)2≥ 0; (b+3)2 ≥ 0 mà (a-1)2+(b+3)2=0
⇒ a-1=0 và b-3=0
⇒ a=1,b=3
a2-2a+6b+b2=-10
<=> a2-2a+6b+b2+10=0
<=> a2-2a+1+6b+b2+9=0
<=> (a-1)2+(b+3)2=0
<=> (a-1)2=(b+3)2=0
\(<=>\left[\begin{array}{} (a-1)^2=0\\ (b+3)^2=0 \end{array} \right.\)
\(<=>\left[\begin{array}{} a-1=0\\ b+3=0 \end{array} \right.\)
\(<=>\left[\begin{array}{} a=1\\ b=-3 \end{array} \right.\)
Vậy a=1;b=-3