`D=R\{0}`
Đặt: `f(x)=2/x+300pix^2`
`f'(x)=(2/x)'+(300pix^2)=-2/x^2+600pix`
`f'(x)=0<=>-2/x^2+600pix=0`
`<=>` \(x=^3\sqrt{\frac{1}{300\pi}}\)
Ta có bảng biến thiên
`=>` Hàm số không có điểm cực đại
Nêu cách tìm cực đại, cực tiểu của hàm số nhờ đạo hàm. Tìm các cực trị của hàm số: y = x 4 - 2 x 2 + 2
Cho hàm số f(x), hình vẽ dưới đây là đồ thị của đạo hàm f’(x).
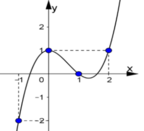
Hàm số g(x)= f(x) - x 3 3 + x 2 - x + 2 đạt cực đại tại điểm nào?
A. x=1
B. x=1
C. x= -1
D. x=2
Cho hàm số y = f ( x ) có đạo hàm f ' ( x ) = x ( x - 1 ) ( x + 2 ) 2 , ∀ x ∈ ℝ . Tìm số điểm cực trị của hàm số đã cho
A. 3
B. 2
C. 4
D. 1
Cho hàm số liên tục trên khoảng (a;b) và x 0 ∈ ( a ; b ) . Có bao nhiêu mệnh đề đúng trong các mệnh đề sau?
(1) Hàm số đạt cực trị tại điểm x 0 khi và chỉ khi f ' ( x 0 ) = 0 .
(2) Nếu hàm số y = f ( x ) có đạo hàm và có đạo hàm cấp hai tại điểm x 0 thỏa mãn điều kiện f ' ( x 0 ) = f ' ' ( x 0 ) = 0 thì điểm x 0 không phải là điểm cực trị của hàm số y = f ( x ) .
(3) Nếu f'(x) đổi dấu khi x qua điểm x 0 thì điểm x 0 là điểm cực tiểu của hàm số y = f ( x ) .
(4) Nếu hàm số y = f ( x ) có đạo hàm và có đạo hàm cấp hai tại điểm x 0 thỏa mãn điều kiện f ' ( x 0 ) = 0 , f ' ' ( x 0 ) > 0 thì điểm x 0 là điểm cực tiểu của hàm số y = f ( x ) .
A. 1
B. 2
C. 0
D. 3
Cho hàm số y=f(x) có đạo hàm f ' x = x 2019 x - 1 2 x + 1 3 . Số điểm cực đại của hàm số f(x) là
A. 1
B. -1
C. 0
D. 3
Cho hàm số f có đạo hàm là f ' ( x ) = x ( x + 1 ) 2 ( x - 2 ) 4 với mọi x ∈ R. Số điểm cực trị của hàm số f là:
A. 0
B. 1
C. 2
D. 3
Cho hàm số y=f(x) có đạo hàm f ' ( x ) = ( x 2 - 1 ) ( x - 4 ) với mọi x ∈ R . Hàm số g ( x ) = f ( 3 - x ) có bao nhiêu điểm cực đại?
A. 0
B. 1
C. 2
D. 3
Cho hàm số f(x) có đạo hàm là f ' ( x ) = x ( x + 1 ) 2 ( x - 2 ) 4 với mọi x ∈ ℝ . Số điểm cực trị của hàm số f(x) là
A. 0
B. 3
C. 2
D. 1
Tìm tất cả các giá trị thực của tham số m để hàm số y = x 3 - 3 m x 2 + 3 ( m 2 - 1 ) x - m 3 + m có cực trị đồng thời khoảng cách từ điểm cực đại của đồ thị hàm số đến gốc tọa độ O bằng 2 lần khoảng cách từ điểm cực tiểu của đồ thị hàm số đến gốc tọa độ O
A. m = - 3 - 2 2 h o ặ c m = - 1
B. m = - 3 + 2 2 h o ặ c m = - 1
C. m = - 3 + 2 2 h o ặ c m = - 3 - 2 2 .
D. m = - 3 + 2 2
Cho hàm số y=f(x) có đạo hàm trên tập K. Khi đó x = x 0 được gọi là điểm cực đại của hàm số y=f(x) nếu
A. f’(x) đổi dấu khi x đi qua giá trị x = x 0 .
B. f’(x) =0.
C. f’(x) đổi dấu từ âm sang dương khi x đi qua giá trị x = x 0 .
D. f’(x) đổi dấu từ dương sang âm khi x đi qua giá trị x = x 0
