Hàm số xác định và có đạo hàm với mọi x ≠ 1.
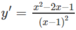
y′=0 ⇔ 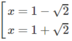
Bảng biến thiên:
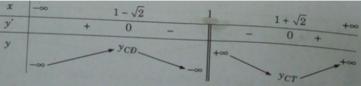
Hàm số đạt cực đại tại x = 1 − 2 và đạt cực tiểu tại x = 1 + 2 , ta có:
y CD = y(1 − 2 ) = −2 2
y CT = y(1 + 2 ) = 2 2
Hàm số xác định và có đạo hàm với mọi x ≠ 1.
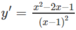
y′=0 ⇔ 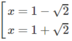
Bảng biến thiên:

Hàm số đạt cực đại tại x = 1 − 2 và đạt cực tiểu tại x = 1 + 2 , ta có:
y CD = y(1 − 2 ) = −2 2
y CT = y(1 + 2 ) = 2 2
Câu 1 : Tìm tất cả các giá trị của tham số thực m để hàm số \(y=mx^3-2mx^2+\left(m-2\right)x+1\) không có cực trị
Câu 2: Tìm tất cả các giá trị thực của tham số m để hàm số \(y=\left(m-1\right)x^4-2\left(m-3\right)x^2+1\) không có cực đại
Câu 3 Để đồ thị hàm số \(y=-x^4-\left(m-3\right)x^2+m+1\) có điểm cực đạt mà không có điểm cực tiểu thì tất cả giá trị thực của tham số m là
Câu 4 Cho hàm số \(y=x^4-2mx^2+m\) .Tìm tất cả các giá trị thực của m để hàm số có 3 cực trị
Cho hàm số y = x 3 - 2 x 2 - 1 (1) và các mệnh đề
(1) Điểm cực trị của hàm số (1) là x = 0 hoặc x = 4/3
(2) Điểm cực trị của hàm số (1) là x = 0 và x = 4/3
(3) Điểm cực trị của đồ thị hàm số (1) là x = 0 và x = 4/3
(4) Cực trị của hàm số (1) là x = 0 và x = 4/3
Trong các mệnh đề trên, số mệnh đề sai là:
A. 0
B. 1
C. 2
D. 3
Tìm các điểm cực trị của các hàm số sau: y = x + ln(x + 1)
Câu 3: Tìm tất cả các giá trị của tham số m để hàm số \(y=x^3-3x^2+mx+1\) đạt cực tiểu tại x=2
Câu 8 : Tìm tất cả các giá trị thực của tham số m để hàm số \(y=\dfrac{1}{3}x^3-mx^2+\left(m+1\right)x-1\) đạt cực đại tại x=\(-\)2
Câu 4: Tìm các giá trị thực của tham số m để hàm số\(y=\dfrac{1}{3}x^3-mx^2+\left(m^2-4\right)x+3\) đạt cực đạt tại x= 3
Câu 6: Tìm các giá trị thực của tham số m để hàm số \(y=\dfrac{1}{3}x^3-mx^2+\left(m^2-4\right)x+3\) đạt cực đạt tại x=3
Tìm cực trị của các hàm số sau: y = x 2 + x - 5 x + 1
Áp dụng Quy tắc 2, hãy tìm các điểm cực trị của hàm số sau: y = sin2x – x