Question

Tìm các khoảng đơn điệu và cực trị của hàm số: \(y=x-3\sqrt[3]{x^2}\)

Answer 1

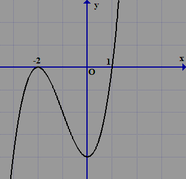
\(y=x-3\sqrt[3]{x^2}\Rightarrow y'=1-\dfrac{2}{\sqrt[3]{x}}=\dfrac{\sqrt[3]{x}-2}{\sqrt[3]{x}}\)

\(y'=0\Leftrightarrow\dfrac{\sqrt[3]{x}-2}{\sqrt[3]{x}}=0\Leftrightarrow x=8\)

\(y'>0\Leftrightarrow\sqrt[3]{x}\left(\sqrt[3]{x}-2\right)>0\Leftrightarrow\left[{}\begin{matrix}x>8\\x< 0\end{matrix}\right.\).

\(y'< 0\Leftrightarrow\sqrt[3]{x}\left(\sqrt[3]{x}-2\right)< 0\Leftrightarrow0< x< 8\).

Vậy y đồng biến trên \(\left(8,+\infty\right)\cup\left(-\infty,0\right)\) ; nghịch biến trên \(\left(0;8\right)\), đạt cực trị tại \(x=8\)