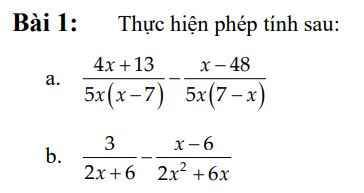\(a,ĐK:x\ne0;x\ne7\\ \dfrac{4x+13}{5x\left(x-7\right)}-\dfrac{x-48}{5x\left(7-x\right)}\\ =\dfrac{4x+13+x-48}{5x\left(x-7\right)}\\ =\dfrac{5x-35}{5x\left(x-7\right)}\\ =\dfrac{5\left(x-7\right)}{5x\left(x-7\right)}\\ =\dfrac{1}{x}\\ b,ĐKx\ne-3\\ \dfrac{3}{2x+6}-\dfrac{x-6}{2x^2+6x}\\ =\dfrac{3}{2x+6}-\dfrac{x-6}{x\left(2x+6\right)}\\ =\dfrac{3x-x+6}{x\left(2x+6\right)}\\ =\dfrac{2x+6}{x\left(2x+6\right)}\\ =\dfrac{1}{x}\)
\(a,\dfrac{4x+13}{5x\left(x-7\right)}-\dfrac{x-48}{5x\left(7-x\right)}=\dfrac{4x+13}{5x\left(x-7\right)}+\dfrac{x-48}{5x\left(x-7\right)}=\dfrac{4x+13+x-48}{5x\left(x-7\right)}=\dfrac{5x-35}{5x\left(x-7\right)}=\dfrac{5\left(x-7\right)}{5x\left(x-7\right)}=\dfrac{1}{x}\)
\(b,\dfrac{3}{2x+6}-\dfrac{x-6}{2x^2+6x}=\dfrac{3}{2x+6}-\dfrac{x-6}{x\left(2x+6\right)}=\dfrac{3x}{x\left(2x+6\right)}-\dfrac{x-6}{x\left(2x+6\right)}=\dfrac{3x-x+6}{x\left(2x+6\right)}=\dfrac{2x+6}{x\left(2x+6\right)}=\dfrac{1}{x}\)