Chọn B.
Ta tính mức thu nhập trung bình của mỗi nhóm
+ Số trung bình của thu nhập gia đình/năm của nhóm 1
+ Số trung bình thu nhập gia đình/năm của nhóm 2
Như vậy; mức thu nhập cùa nhóm 2 cao hơn.
Có ba nhóm máy A, B, C dùng để sản xuất ra hai loại sản phẩm I và II. Để sản xuất một đơn vị sản phẩm mỗi loại lần lượt phải dùng các máy thuộc các nhóm khác nhau. Số máy trong một nhóm và số máy của từng nhóm cần thiết để sản xuất ra một đơn vị sản phẩm thuộc mỗi loại được dùng cho trong bảng sau:
| Nhóm | Số máy trong mỗi nhóm | Số máy trong từng nhóm để sản xuất ra một đơn vị sản phẩm | |
| Loại I | Loại II | ||
| A | 10 | 2 | 2 |
| B | 4 | 0 | 2 |
| C | 12 | 2 | 4 |
Một đơn vị sản phẩm I lãi 3 nghìn đồng, một đơn vị sản xuất II lãi 5 nghìn đồng. Hãy lập kế hoạch sản xuất để cho tổng số tiền lãi cao nhất.
Cho các số liệu thống kê được ghi trong hai bảng sau
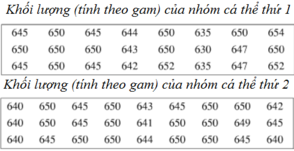
a) Lập bảng phân bố tần số và tần suất ghép lớp theo nhóm cá thứ 1 với các lớp là
[630; 635) ; [635;640) ; [640; 645) ; [645; 650) ; [650; 655)
b) Lập bảng phân bố tần số và tần suất ghép lớp theo nhóm cá thứ 2 với các lớp là:
[638;642) ; [642; 646) ; [646;650) ; [650; 654] ;
c) Mô tả bảng phân bố tần suất ghép lớp đã được lập ở câu a) bằng cách vẽ biểu đồ tần suất hình cột và đường gấp khúc tần suất
d) Mô tả bảng phân bố tần suất ghép lớp đã được lập ở câu b) bằng cách vẽ biểu đồ tần số hình cột và đường gấp khúc tần số
e) Tính số trung bình cộng, phương sai và độ lệch chuẩn của các bảng phân bố đã lập được
Từ đó, xét xem nhóm cá nào có khối lượng đồng đều hơn
Cho bảng phân bố tần số
Mức thu nhập trong năm 2000 của 31 gia đình trong một bản ở vùng núi cao
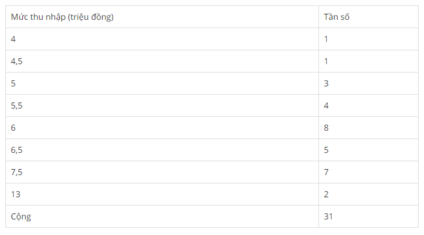
Chọn giá trị đại diện cho các số liệu thống kê đã cho
Cho bảng phân bố tần số
Mức thu nhập trong năm 2000 của 31 gia đình trong một bản ở vùng núi cao
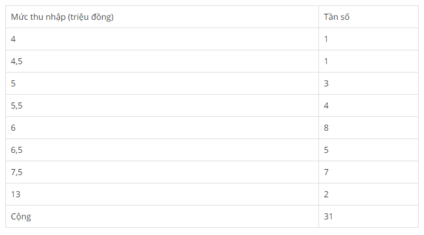
Tính số trung bình, số trung vị, mốt của các số liệu thống kê đã cho.
Cho hai bảng phân bố tần số ghép lớp
Khối lượng của nhóm cá mè thứ 1
| Lớp khối lượng(kg) | [0,6;0,8) | [0,8;1,0) | [1,0;1,2) | [1,2;1,4] | Cộng |
| Tần số | 4 | 6 | 6 | 4 | 20 |
Khối lượng của nhóm cá mè thứ 2
| Lớp khối lượng(kg) | [0,5;0,7) | [0,7;0,9) | [0,9;1,1) | [1,1;1,3) | [1,3;1,5] | Cộng |
| Tần số | 3 | 4 | 6 | 4 | 3 | 20 |
a) Tính các số trung bình cộng của các bảng phân bố tần số ghép lớp đã cho.
b) Tính phương sai của các bảng phân bố tần số ghép lớp đã cho.
c) Xét xem nhóm cá nào có khối lượng đồng đều hơn?
Giả sử trường Trung học phổ thông M còn có một nhóm học sinh nam lớp 10 chuyên toán (kí hiệu là nhóm T) có chiều cao trung bình là x = 163 cm, có độ lệch chuẩn là s = 13. So sánh chiều cao của ba nhóm học sinh đã cho (nhóm nam, nhóm nữ, nhóm T).
So sánh chiều cao của học sinh nam với chiều cao của học sinh nữ trong nhóm học sinh được khảo sát.
Có một hội gồm n cặp vợ chồng (n≥3) đôi một quen biết lẫn nhau. Hàng năm, vào ngày 20/10, mỗi ông chồng đều tặng một số bông hồng (ít nhất là một bông) cho mỗi bà vợ trong hội (kể cả vợ mình). Một bà vợ sẽ cảm thấy bực mình, nếu số bông hồng mà bà ấy được chồng mình tặng ít hơn tổng số bông hồng mà ông ấy tặng n−1 bà vợ khác trong hội. Sau ngày 20/10 năm nay, người ta thấy rằng, có thể phân chia chia tất cả n ông chồng thành hai nhóm, sao cho với mỗi bà vợ, tổng số bông hồng mà bà ấy được các ông chồng thuộc nhóm này tặng đúng bằng tổng số bông hồng mà bà ấy được các ông chồng thuộc nhóm kia tặng. Chứng minh rằng, trong ngày 20/10 năm nay, đã có ít nhất một bà vợ trong hội cảm thấy bực mình.
Số lỗi sai trong 1 bài kiểm tra 1 tiết của 1 nhóm học sinh được ghi lại như sau:
1, 3, 3, 4, 4, 6, 7, 7, 7, 8, 10
Lập bảng phân bố tần số- tần suất ghép lớp: [1, 4]; [5, 6]; [7, 8]; [9, 10]
Tính phương sai của nhóm
A. 6,39
B. 6,93
C. 5,93
D. 6,99
