Giả thuyết Goldbach tam nguyên. Và chưa ai có thể chứng minh điều này.
Đúng 0
Bình luận (0)
Các câu hỏi tương tự
Năm 1742, Christian Goldbach đã gửi cho đồng nghiệp một bức thư. Trong thư, ông đề cập đến các vấn đề liên quan đến thuyết số: “Tất cả các số nguyên lớn hơn 2 đều là tổng của 3 số nguyên tố”. Ví dụ như 77 là tổng của các số nguyên tố 53, 11 và 13 hay 35 bằng tổng của các số nguyên tố 3, 13, 19.
Vì sao mọi số nguyên lớn hơn 2 đều có tổng của các số nguyên tố ví dụ:45=43+2(câu hỏi này cho người siêu thông minh)
Gọi A là tổng các chữ số của một số có 2018 chữ số, B là tổng các chữ số của A và C là tổng các chữ số của B. Gọi * là giá trị lớn nhất có thể có của C. Lấy số nguyên dương nhỏ nhất chia hết cho 11 và có tích các chữ số bằng (3x * + 2) chia cho 13. Số dư còn lại sau khi chia là **. Tìm * và **.
Xem chi tiết
Gọi S là tập hợp tất cả các giá trị thực của tham số m để đồ thị hàm số
y
-
x
-
1
3
+
3
m
x
-
1
-
2
có hai điểm cực trị cách đều gốc tọa độ. Tổng các giá trị tuyệt đối của tất cả các phần tử t...
Đọc tiếp
Gọi S là tập hợp tất cả các giá trị thực của tham số m để đồ thị hàm số y = - x - 1 3 + 3 m x - 1 - 2 có hai điểm cực trị cách đều gốc tọa độ. Tổng các giá trị tuyệt đối của tất cả các phần tử thuộc S là
A. 4.
B. 2 3
C. 1.
D. 5.
Đề bài:Ba thành viên trong đội bóng nữ trường trung học Euclid nói chuyện với nhau.Ashley: Tớ vừa nhận ra số áo của bọn mình đều là những số nguyên tố có hai chữ số.Bethany: Tổng hai số áo của các bạn là ngày sinh của tớ vừa diễn ra trong tháng này.Caitlin: Ừ, vui thật, tổng hai số áo của các cậu lại là ngày sinh của tớ vào cuối tháng này.Ashley: Và tổng số áo của các cậu lại đúng bằng ngày hôm nay.Vậy Caitlin mặc áo số mấy?(A) 11 (B) 13 (C) 17 (D) 19 (E) 23
Đọc tiếp
Đề bài:
Ba thành viên trong đội bóng nữ trường trung học Euclid nói chuyện với nhau.
Ashley: Tớ vừa nhận ra số áo của bọn mình đều là những số nguyên tố có hai chữ số.
Bethany: Tổng hai số áo của các bạn là ngày sinh của tớ vừa diễn ra trong tháng này.
Caitlin: Ừ, vui thật, tổng hai số áo của các cậu lại là ngày sinh của tớ vào cuối tháng này.
Ashley: Và tổng số áo của các cậu lại đúng bằng ngày hôm nay.
Vậy Caitlin mặc áo số mấy?
(A) 11 (B) 13 (C) 17 (D) 19 (E) 23
Cho hàm số y= x4- (2m-1) x2+2m có đồ thị (C) . Có tất cả bao nhiêu giá trị nguyên của tham số m để đường thẳng d: y= 2 cắt đồ thị (C) tại bốn điểm phân biệt đều có hoành độ lớn hơn 3 là
A. 1
B. 2
C. 3
D. 4
Trong tất cả các điểm có tọa độ nguyên thuộc đồ thị (C) của hàm số 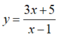 , số điểm có hoành độ lớn hơn tung độ là
, số điểm có hoành độ lớn hơn tung độ là
A.2
B.8
C.6
D.4
Cho hàm số
y
f
x
có đồ thị như hình bên dưới Gọi S là tập hợp tất cả các giá trị nguyên của tham số
m
∈
-
100
;
100
để hàm số
h
x
f
2
x
+
2...
Đọc tiếp
Cho hàm số y = f x có đồ thị như hình bên dưới
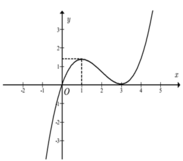
Gọi S là tập hợp tất cả các giá trị nguyên của tham số m ∈ - 100 ; 100 để hàm số h x = f 2 x + 2 + 4 f x + 2 + 3 m có đúng 3 điểm cực trị. Tổng giá trị của tất cả các phần tử thuộc S bằng
![]()
![]()
![]()
![]()
Tìm tất cả các giá trị của tham số m để hàm số
f
x
4
sin
x
+
6
m
+
sin
x
9
sin
x...
Đọc tiếp
Tìm tất cả các giá trị của tham số m để hàm số f x = 4 sin x + 6 m + sin x 9 sin x + 4 1 + sin x có giá trị lớn nhất không nhỏ hơn 1 3
A. m ≥ log 6 2 3
B. m ≥ log 6 13 18
C. m ≤ log 6 3
D. m ≤ log 6 2 3









