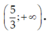Chọn C
Vì hàm số
y
=
(
3
x
-
5
)
1
3
có số mũ không nguyên nên hàm số xác định khi 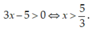
Vậy tập xác định của hàm số
y
=
(
3
x
-
5
)
1
3
là