Điều kiện xác định: 2 - x ≥ 0 5 - x ≥ 0 ⇔ x ≤ 2 x ≤ 5 ⇔ x ≤ 2
Tập xác định của hàm số là: D = ( - ∞ ;2]
Đúng 0
Bình luận (0)
Các câu hỏi tương tự
Tìm tập xác định của hàm số
y
x
2
+
x
-
2
x
2
-
1
A. x -2; x ≤ -2; B. x ≤ -2; x ≥ -1 C. x ≤ -2; x ≤ -2; D. x ≤ -2; -1 x 1; x 1
Đọc tiếp
Tìm tập xác định của hàm số y = x 2 + x - 2 x 2 - 1
A. x < -2; x ≤ -2;
B. x ≤ -2; x ≥ -1
C. x ≤ -2; x ≤ -2;
D. x ≤ -2; -1 < x < 1; x > 1
Tìm tập xác định D của hàm số
y
x
+
2
-
x
+
3
A. B. C. D R. D.
Đọc tiếp
Tìm tập xác định D của hàm số y = x + 2 - x + 3
A. 
B. 
C. D = R.
D. 
Tìm tập xác định D của hàm số
y
x
+
2
−
x
+
3
A. D
[
−
3
;
+
∞
)
B. D
[
−
2
;
+
∞
)
C. D R D. D
[
2
;
+
∞
)
Đọc tiếp
Tìm tập xác định D của hàm số y = x + 2 − x + 3
A. D = [ − 3 ; + ∞ )
B. D = [ − 2 ; + ∞ )
C. D = R
D. D = [ 2 ; + ∞ )
Tìm tập xác định D của hàm số y = \(\dfrac{\sqrt{x+2}}{x\sqrt{x^2-4x+4}}\)
Cho hàm số y f(x) với tập xác định D. Trong các phát biểu sau đây phát biểu nào đúng? A. Giá trị lớn nhất của hàm số đã cho là số lớn hơn mọi giá trị của hàm số. B. Nếu f(x) ≤ M, ∀x ∈ D thì M là giá trị lớn nhất của hàm số y f(x).
C. Số M f(
x
0
) trong đó
x
0
∈ D là giá trị lớn nhất của hàm số y f(x) nếu M f(x), ∀x ∈ D D. Nếu tồn tại
x
0
∈ D...
Đọc tiếp
Cho hàm số y = f(x) với tập xác định D. Trong các phát biểu sau đây phát biểu nào đúng?
A. Giá trị lớn nhất của hàm số đã cho là số lớn hơn mọi giá trị của hàm số.
B. Nếu f(x) ≤ M, ∀x ∈ D thì M là giá trị lớn nhất của hàm số y = f(x).
C. Số M = f( x 0 ) trong đó x 0 ∈ D là giá trị lớn nhất của hàm số y = f(x) nếu M > f(x), ∀x ∈ D
D. Nếu tồn tại x 0 ∈ D sao cho M = f( x 0 ) và M ≥ f(x),∀x ∈ D thì M là giá trị lớn nhất của hàm số đã cho.
Tập xác định của hàm số sau là
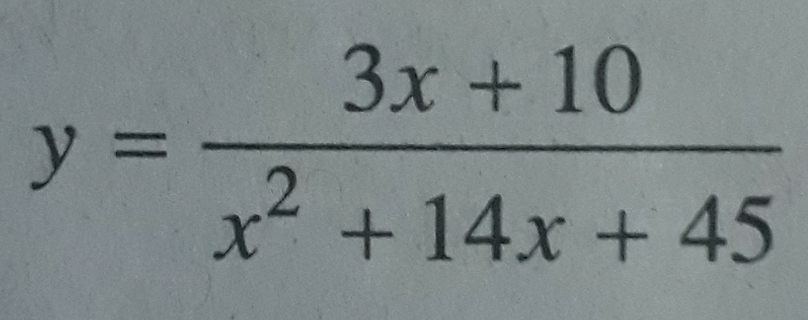
A. R
B. R \ {-5; 9}
C. R \ {-5, -9}
D. R \ {5; 9}
Tập xác định của hàm số
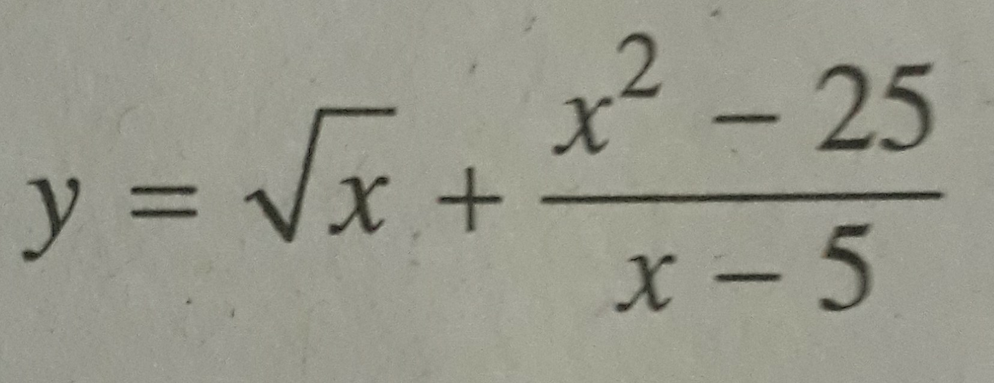
A. R B. [0; +∞) C. [0; +∞) \ {5} D. [0; 5)
tìm tập xác định của hàm số y=\(\sqrt{-2x^2+5x-2}\)
A. D=\((-\infty;\dfrac{1}{2}]\) B. \([2;+\infty)\) C. \((-\infty;\dfrac{1}{2}]\)u\([2;+\infty)\) D. \([\dfrac{1}{2};2]\)
giải chi tiết
Câu 1.
a) Cho tập A,B lần lượt là tập xác định của hàm số f(x) = \(\sqrt{6-x}\) và g(x) = \(\dfrac{3}{2x+1}\). Xác định các tập A∩B, A∪B, A∖B, CRA.
b) Cho tập hợp C=[−3;8] và D=[m−6;m+3). Với giá trị nào của m thì C∩D là một đoạn thẳng có độ dài bằng 4.
Cho hình bình hành ABCD. Biết I (7/2;5/2) là trung điểm của cạnh CD, D (3;3/2) và đường phân giác góc BAC có phương trình là d: x-y+1=0. Xác định tọa độ đỉnh B.