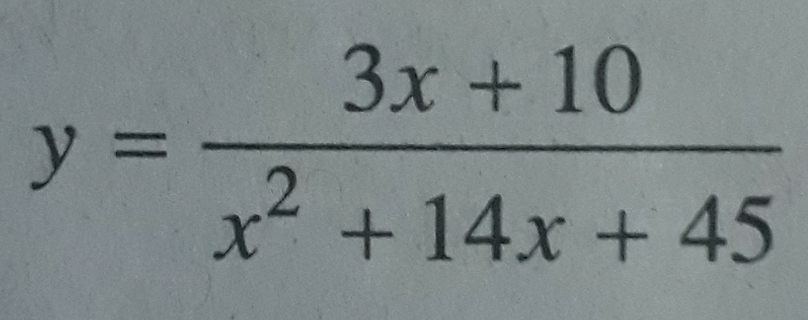Đáp án: C ( v ì x 2 + 14 x + 45 ≠ 0 ⇔ x ≠ - 5 v à x ≠ - 9 ) .
Đúng 0
Bình luận (0)
Các câu hỏi tương tự
Tập xác định của hàm số
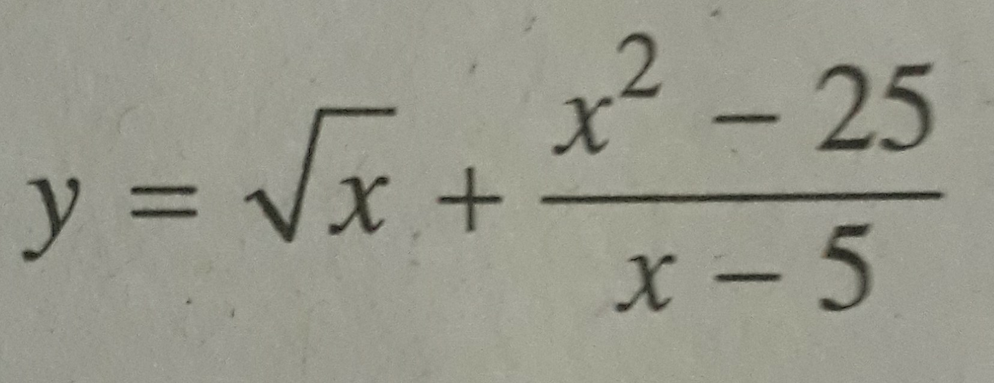
A. R B. [0; +∞) C. [0; +∞) \ {5} D. [0; 5)
Cho các tập \(B=\left\{x\in\mathbb{R}\text{|}-5\le x\le5\right\};C=\left\{x\in\mathbb{R}\text{|}x\le a\right\};D=\left\{x\in\mathbb{R}\text{|}x\ge b\right\}\). Xác định a, b biết \(C\cap B,D\cap B\) lần lượt là các đoạn có độ dài lần lượt bằng 5 và 9.
Xác định các tập sau
a) ( -3; 5 ] giao với R
b) (1;2) hợp với R
c) [ -3;5 ] giáo với. Z
Hàm số nào có tập xác định D R. A.
y
2
x
+
3
x
-
1
B.
y
2
x
+
3
4
x
-
8
C.
y
10...
Đọc tiếp
Hàm số nào có tập xác định D= R.
A. y = 2 x + 3 x - 1
B. y = 2 x + 3 4 x - 8
C. y = 10 x - 20 x 2 + 1
D. y = 2 x + 4 + x 2 - 16
Bài 4.Tập hợp nào dưới đây là tập rỗng:a)A{varnothing}b)B{xinR|x2+10}c)C{xinR|x -3 và x6}Bài 5.Tìm tất cả tập con của các tập hợp sau: a)A{3;5;7}b)B{a;b;c;d}c)C{varnothing}d)D{xinR|(x-1)(x2-5x+6)0}Bài 6. Cho các tập hợp: A{a;b;c;d}, B{a;b}. Hãy tìm tất cả các tập X sao cho: BsubsetXsubsetA.
Đọc tiếp
Bài 4.Tập hợp nào dưới đây là tập rỗng:
a)A={\(\varnothing\)}
b)B={x\(\in\)R|x2+1=0}
c)C={x\(\in\)R|x< -3 và x>6}
Bài 5.Tìm tất cả tập con của các tập hợp sau:
a)A={3;5;7}
b)B={a;b;c;d}
c)C={\(\varnothing\)}
d)D={x\(\in\)R|(x-1)(x2-5x+6)=0}
Bài 6. Cho các tập hợp: A={a;b;c;d}, B={a;b}. Hãy tìm tất cả các tập X sao cho: B\(\subset\)X\(\subset\)A.
Bài 1. Liệt kê các phần tử của tập hợp sau:a) A {x Î N | x 6} b) B {x Î N | 1 x £ 5}c) C {x Î Z , |x| £ 3} d) D {x Î Z | x2 - 9 0}e) E {x Î R | (x - 1)(x2 + 6x + 5) 0} f) F {x Î R | x2 - x + 2 0}g) G {x Î N | (2x - 1)(x2 - 5x + 6) 0} h) H {x | x 2k với k Î Z và -3 k 13}i) I {x Î Z | x2 4 và |x| 10} j) J {x | x 3k với k Î Z và -1 k 5}k) K {x Î R | x2 - 1 0 và x2 - 4x + 3 0} l) L {x Î Q | 2x - 1 0 hay x2 - 4 0
Đọc tiếp
Bài 1. Liệt kê các phần tử của tập hợp sau:
a) A = {x Î N | x < 6} b) B = {x Î N | 1 < x £ 5}
c) C = {x Î Z , |x| £ 3} d) D = {x Î Z | x2 - 9 = 0}
e) E = {x Î R | (x - 1)(x2 + 6x + 5) = 0} f) F = {x Î R | x2 - x + 2 = 0}
g) G = {x Î N | (2x - 1)(x2 - 5x + 6) = 0} h) H = {x | x = 2k với k Î Z và -3 < k < 13}
i) I = {x Î Z | x2 > 4 và |x| < 10} j) J = {x | x = 3k với k Î Z và -1 < k < 5}
k) K = {x Î R | x2 - 1 = 0 và x2 - 4x + 3 = 0} l) L = {x Î Q | 2x - 1 = 0 hay x2 - 4 = 0
Xác định các tập hợp sau và biểu diễn chúng trên trục số
R \ ((3; 5) ∩ (4; 6))
Tập hợp tất cả các giá trị của tham số m để hàm số y= mx + 9 nghịch biến trên R là
Viết mỗi tập hợp sau bằng cách liệt kê các phần tử
a) A= {x ∈ R | (2x – x2)( 3x – 2) = 0}
b, B = { x∈ Z | 2x3-3x2-5x = 0 }
c , C= { x ∈ Z | 2x2 -75x -77 = 0 }
d , D = { x ∈ R | (x2 - x - 2 ) (x2 - 9 ) = 0 } .