Chọn C.
Bất phương trình 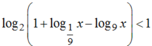
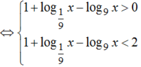


Suy ra tập nghiệm S của bất phương trình là ![]() .
.
Chọn C.
Bất phương trình 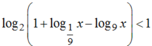
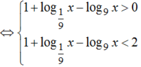


Suy ra tập nghiệm S của bất phương trình là ![]() .
.
Cho hai số dương a và b. Đặt X = log a + b 2 , Y = log a + log b 2 . Khẳng định nào dưới đây là đúng
![]()
![]()
![]()
![]()
Biết rằng tập nghiệm S của bất phương trình log - x 2 + 100 x - 2400 < 2 có dạng S = a ; b \ x 0 . Giá trị của a + b - x 0 bằng:
A. 100
B. 30
C. 150
D. 50
Giả sử a, b là các số thực sao cho x3 + y3 = a.103x + b.102x đúng với mọi số thực dương x, y, z thỏa mãn log (x + y) = z và log(x2 + y2) = z + 1. Giá trị của a+b bằng:
A. - 31 2
B. - 25 2
C. 31 2
D. 29 2
Tập nghiệm của bất phương trình log 2 x - 1 ≥ log x là
![]()
![]()
![]()
![]()
Cho các số thực dương a,b thỏa mãn log a = x , log b = y . Tính P = log ( a 2 b 3 )
![]()
![]()
![]()
![]()
Có bao nhiêu giá trị nguyên dương của x thỏa mãn bất phương trình dưới đây:
log (x - 40) + log (60 - x) < 2?
A. 20
B. 10
C. Vô số
D. 18
Tập nghiệm của bất phương trình log 0 , 7 log 6 x 2 + x x + 4 < 0 có dạng a ; b ∪ c ; + ∞ với a; b; c là các số nguyên. Tính tổng S = a + b + c .
A. 1
B. -1
C. -7
D. 7
Cho a là số nguyên dương lớn nhất thỏa mãn \(3{\log _3}\left( {1 + \sqrt a + \sqrt[3]{a}} \right) > 2{\log _2}\sqrt a\).Tìm phần nguyên của \({\log _2}\left( {2017a} \right)\)
A.14
B.22
C.16
D.19
cho hai số a,b là hai số thực đều lớn hơn 1. giá trị nhỏ nhất của biểu thức s=
\(\dfrac{1}{log_{b\sqrt[3]{a}}}\)+\(\dfrac{1}{log\sqrt[3]{ab^2}}\)