Các câu hỏi tương tự
Gọi S1 là tập nghiệm của bất phương trình
log
2
(
x
+
5
)
+
log
1
2
(
3
-
x
)
≥
0
và S2 là tập nghiệm của bất phương trình log2(x + 1) ≥ 1. Khẳng định nào dưới đây đúng ? A.
S
1
∩
S
2
[...
Đọc tiếp
Gọi S1 là tập nghiệm của bất phương trình log 2 ( x + 5 ) + log 1 2 ( 3 - x ) ≥ 0 và S2 là tập nghiệm của bất phương trình log2(x + 1) ≥ 1. Khẳng định nào dưới đây đúng ?
A. S 1 ∩ S 2 = [ 1 ; 3 )
B. S 1 ∩ S 2 = [ - 1 ; 3 )
C. S 1 ∩ S 2 = - 1 ; 1
D. S 1 ∩ S 2 = 1 ; 3
Tập nghiệm của bất phương trình
1
3
x
+
2
3
-
x
là A.
1
,
2
. B.
2
,
+
∞...
Đọc tiếp
Tập nghiệm của bất phương trình 1 3 x + 2 > 3 - x là
A. 1 , 2 .
B. 2 , + ∞ .
C. [ 2 , + ∞ ) .
D. ( 1 , 2 ]
Tập nghiệm S của bất phương trình
log
1
2
3
x
-
2
log
1
2
4
-
x
là A.
S
3
2
;
4
B.
S...
Đọc tiếp
Tập nghiệm S của bất phương trình log 1 2 3 x - 2 > log 1 2 4 - x là
A. S = 3 2 ; 4
B. S = - ∞ ; 3 2
C. S = 2 3 ; 3
D. S = 2 3 ; 3 2
Tập nghiệm của bất phương trình log0,5 (x - 1) log0,5 2 là:
Đọc tiếp
Tập nghiệm của bất phương trình log0,5 (x - 1) > log0,5 2 là:
![]()
![]()
![]()
![]()
Tập nghiệm của bất phương trình
log
2
x
+
1
-
2
log
4
5
-
x
1
-
log
2
x
-
2
là A. (3;5) B. (2;3) C. (2;5) D. (-4;3)
Đọc tiếp
Tập nghiệm của bất phương trình
log 2 x + 1 - 2 log 4 5 - x < 1 - log 2 x - 2 là
A. (3;5)
B. (2;3)
C. (2;5)
D. (-4;3)
Tập nghiệm của bất phương trình
2
log
3
(
x
-
1
)
+
log
3
(
2
x
-
1
)
≤
2
là A. S (1; 2] B. S
(
-
1
2
;
2
)
C. [1; 2] D.
[...
Đọc tiếp
Tập nghiệm của bất phương trình 2 log 3 ( x - 1 ) + log 3 ( 2 x - 1 ) ≤ 2 là
A. S = (1; 2]
B. S = ( - 1 2 ; 2 )
C. [1; 2]
D. [ - 1 2 ; 2 ]
Tập nghiệm của bất phương trình log(x2 + 25) > log(10x) là
![]()
![]()
![]()
![]()
Với m là tham số thực dương khác 1. Hãy tìm tập nghiêm S của bất phương trình logm(2x2 + x + 3)
≤
logm(3x2 - x). Biết rằng x 1 là một nghiệm của bất phương trình.
Đọc tiếp
Với m là tham số thực dương khác 1. Hãy tìm tập nghiêm S của bất phương trình logm(2x2 + x + 3) ≤ logm(3x2 - x). Biết rằng x = 1 là một nghiệm của bất phương trình.
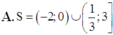
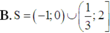
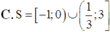
![]()
Tập nghiệm của bất phương trình
log
2
(
x
+
1
)
1
là A.
(
-
1
,
+
∞
)
B.
(
-
∞
,
1
)
C.
(
-
1
,
2...
Đọc tiếp
Tập nghiệm của bất phương trình log 2 ( x + 1 ) < 1 là
A. ( - 1 , + ∞ )
B. ( - ∞ , 1 )
C. ( - 1 , 2 )
D. (-1,1)




