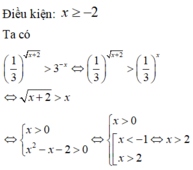
Kết hợp điều kiện, vậy tập nghiệm của bất phương trình là S = 2 ; + ∞
Đáp án A
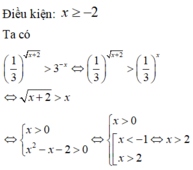
Kết hợp điều kiện, vậy tập nghiệm của bất phương trình là S = 2 ; + ∞
Đáp án A
Gọi S1 là tập nghiệm của bất phương trình log 2 ( x + 5 ) + log 1 2 ( 3 - x ) ≥ 0 và S2 là tập nghiệm của bất phương trình log2(x + 1) ≥ 1. Khẳng định nào dưới đây đúng ?
A. S 1 ∩ S 2 = [ 1 ; 3 )
B. S 1 ∩ S 2 = [ - 1 ; 3 )
C. S 1 ∩ S 2 = - 1 ; 1
D. S 1 ∩ S 2 = 1 ; 3
Tập nghiệm của bất phương trình 2 x + 2 ( x + 1 ) ≤ 3 x + 3 ( x - 1 )
A. x ∈ [ 2 ; + ∞ )
B. x ∈ 2 ; + ∞
C. x ∈ - ∞ ; 2
D. 2 ; + ∞
Tập nghiệm của bất phương trình 2 x + 2 ( x + 1 ) ≤ 3 x + 3 ( x - 1 )
A. x ∈ [ 2 ; + ∞ )
B. x ∈ 2 ; + ∞
C. x ∈ - ∞ ; 2
D. 2 ; + ∞
Tìm tập nghiệm của bất phương trình: 2 2 x 8 > 1
A. x > 3/2 B. x < 3/2
C. x > 2/3 D. x < 2/3
Tìm tập nghiệm của bất phương trình:
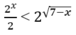
A. x < 3 B. x ≥ 1
C. 1 ≤ x < 3 D. x < 1
Tập nghiệm của bất phương trình 1 3 x + 2 > 3 − x
A. 0 ; 2 .
B. 2 ; + ∞ .
C. − 2 ; − 1 .
D. 0 ; + ∞ .
Tìm tập nghiệm của bất phương trình:
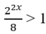
A. x > 3/2 B. x < 3/2
B. x > 2/3 D. x < 2/3
Tìm tập nghiệm S của bất phương trình log0,2 (x – 1) < log0,2 (3 – x).
A. S = - ∞ ; 3
B. S = 2 ; 3
C. S = 2 ; + ∞
D. S = 1 ; 2
Tập nghiệm của bất phương trình 1 3 x + 2 > 3 - x là
A. 1 , 2 .
B. 2 , + ∞ .
C. [ 2 , + ∞ ) .
D. ( 1 , 2 ]