Chọn: D
![]()
Ta có: y ' = m 2 - m - 2 x + m 2
Để hàm số nghịch biến trên khoảng 1 ; + ∞ thì

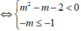
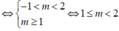
Vậy m ∈ [ 1 ; 2 )
Chọn: D
![]()
Ta có: y ' = m 2 - m - 2 x + m 2
Để hàm số nghịch biến trên khoảng 1 ; + ∞ thì

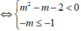
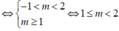
Vậy m ∈ [ 1 ; 2 )
Tập hợp S tất cả các giá trị của tham số thực m để hàm số: y = 1 3 x 3 - ( m + 1 ) x 2 + ( m 2 + 2 m ) x - 3 nghịch biến trên khoảng (-1;1) là
A. S = ∅
B. S = [0;1]
C. S = [-1;0]
D. S = {-1}
Tập hợp tất cả các giá trị thực của tham số m để hàm số y = - x 3 - 6 x 2 + ( 4 m + 9 ) x + 4 nghịch biến trên khoảng (- ∞ ; 1) là
A. (- ∞ ; 0]
B. [- 3 4 ;+ ∞ )
C. (- ∞ ;- 3 4 ]
D. (0;+ ∞ ]
Tìm tất cả các giá trị thực của tham số m để hàm số y = - x 3 + 2 x 2 - ( m - 1 ) x + 2 nghịch biến trên khoảng (-∞;+∞)
A. m ≤ 7 3
B. m ≥ 7 3
C. m ≥ 1 3
D. m > 7 3
Tập hợp tất cả các giá trị của tham số m để hàm số y = ln 3 x - 1 - m x + 2 nghịch biến trên khoảng ( 1 2 ; 3 ] là:
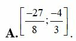
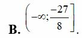

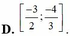
Tập hợp tất cả các giá trị của tham số m để hàm số y = ln 3 x - 1 - m 2 + 2 nghịch biến trên khoảng ( 1 2 ; 3 ] là:
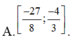
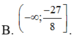
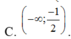

Cho hàm số y = 2 x + 1 + 1 2 x - m với m là tham số thực. Gọi S là tập hợp tất cả các giá trị nguyên của tham số m trong khoảng (-50;50) để hàm số nghịch biến trên khoảng (-1;1). Số phần tử của tập hợp S là:
A. 47
B. 48
C. 50
D. 49
Tập hợp tất cả các giá trị thực của tham số m để hàm số y = - x 3 - 6 x 2 + 4 m - 9 x + 4 nghịch biến trên khoảng - ∞ ; - 1 là
A. ( - ∞ ; 0 ]
B. [ - 3 4 ; + ∞ )
C. ( - ∞ ; - 3 4 ]
D. [ 0 ; + ∞ )
Tìm tất cả các giá trị thực của tham số m để hàm số y = x + 2 - m x + 1 nghịch biến trên các khoảng mà nó xác định?
A. m ≤ -1
B. m < 1.
C. m < -3.
D. m ≤ -3
Tìm tất cả các giá trị thực của tham số m để hàm số y = x + 2 - m x + 1 nghịch biến trên mỗi khoảng xác định của nó.
![]()
![]()
![]()
![]()