Xét ΔAMB và ΔAMC, ta có:
AB = AC (gt)
BM = CM (vì M là trung điểm BC)
AM cạnh chung
Suy ra: ΔAMB = ΔAMC (c.c.c)
Suy ra: ∠(AMB) = ∠(AMC) (1)
Lại có: ∠(AMB) + ∠(AMC) = 180o (hai góc kề bù) (2)
Từ (1) và (2) suy ra: ∠(AMB) = ∠(AMC) = 90o
Vậy AM ⊥ BC.
Tam giác ABC cân tại A có AB=AC=34cm, BC=32cm. Kẻ đường trung tuyến AM a) Chứng minh rằng AM vuông góc BC b) Tính độ dài AM c)Kẻ MF vuông góc AB;ME vuông góc AC. C/m FE song song BC d)so sánh BM và ME
Tam giác ABC cân tại A có AB=AC=34cm, BC=32cm. Kẻ đường trung tuyến AM a) Chứng minh rằng AM vuông góc BC b) Tính độ dài AM c)Kẻ MF vuông góc AB;ME vuông góc AC. C/m FE song song BC d)so sánh BM và ME
Tam giác ABC cân tại A có AB = AC = 34cm, BC = 32cm. Kẻ đường trung tuyến AM. Tính độ dài AM
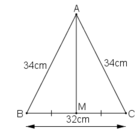
Cho tam giác BC cân tại A, AB=AC=34cm, BC=32cm. Kẻ đường trung tuyến AM
a. Chứng minh AM vuông góc BC
b. Tính AM
Tam giác ABC cân tại A có AB = AC = 34cm, BC = 32cm. Kẻ đường trung tuyến AM.
a) Chứng minh rằng AM⊥BCAM⊥BC
b) Tính độ dài AM.
nhah thì mk tk cho câu này tr sác cs
cho tam giác ABC cân tại A có AB=AC=34cm, BC=32cm. Kẻ trung tuyến AM. Tính AM?
Cho tam giác ABC cân tại A có AB=AC=34cm; BC=32cm. Kẻ trung tuyến AM. Tính AM
1) tam giác ABC có các đường trung tuyến BD và CE bằng nhau . chứng minh rằng tam giác ABC là tam giác cân.
2)cho tam giác ABC cân ở A , AB=34cm , BC =32cm , và 3 trung tuyến AM , BN , CP đồng quy tại trọng tâm G
a) chúng minh AM vuông góc với
b) tính độ dài AM , BN ,CP (làm trong kết quả đến chữ số thập phân thứ 2)
Bài 1: cho tam giác ABC cân tại A có AB=AC=34cm, BC=32cm. Kẻ đường trung tuyến AM.
a) Chứng minh AM vuông góc vs BC
b) Tính độ dài AM.
Bài 2: Cho tam giác ABC, đường trung tuyến AM. Gọi I là trung điểm của BM. Trên tia đối của tia IA lấy điểm E sao cho IE=IA.
a) Điểm M là trọng tâm của tam giác nào ?
b) Gọi F là trung điểm của CE. Chứng minh ba điểm A, M, F thẳng hàng.
